Improper Integrals

Improper Integrals over \([a, \infty)\) and \((-\infty, b]\)

Definition

Let \(f\) be a continuous function on the unbounded interval \([a, \infty)\). The improper integral of \(f\) over the interval \([a, \infty)\) is defined by

\[\int_a^\infty f(x) ~dx = \lim_{t \rightarrow \infty} \int_a^t f(x) ~dx\]

if the limit exists. Similarly, the improper integral of \(f\) over the interval \((-\infty, b]\) is defined by

\[\int_{-\infty}^b f(x) ~dx = \lim_{s \rightarrow -\infty} \int_s^b f(x) ~dx\]

if the limit exists.

Geometric Interpretation of an Improper Integral

If an improper integral exists, it corresponds to the area of a region that is unbounded on the left or on the right.

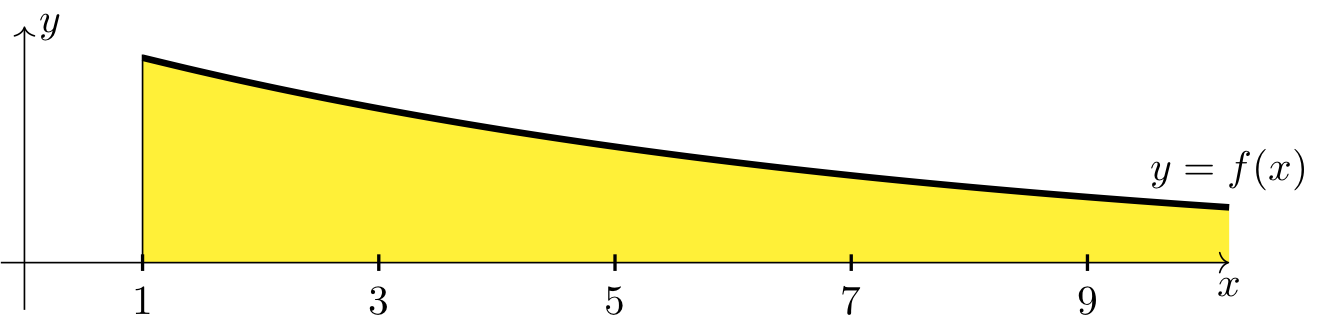
Fig. 16 Improper integral unbounded on the right

Long Text Description

There is a horizontal x axis with the points 1, 3, 5, 6, and 9 labeled. There is a vertical y axis. The decreasing, concave up curve y = f(x) is plotted on these axes. The region between the curve and the x axis, beginning at x = 1 on the left, is shaded yellow.

Example 1

Improper integral unbounded on the right

Evaluate \(\displaystyle \int_2^\infty \frac{1}{x} ~dx\), if it exists.

Step 1: Evaluate \(\displaystyle \int_2^t \frac{1}{x} ~dx\).

\[\begin{align*} \int_2^t \frac{1}{x} ~dx &= \ln|x|\Big|_2^t \\ &= \ln t - \ln 2 \end{align*}\]

Step 2: Use Step 1 to evaluate \(\displaystyle \int_2^\infty \frac{1}{x} ~dx\) as the limit of a definite integral.

\[\begin{align*} \int_2^\infty \frac{1}{x} ~dx &= \lim_{t \rightarrow \infty} \int_2^t \frac{1}{x} ~dx\\ &= \lim_{t \rightarrow \infty}(\ln t - \ln 2) && \hbox{using Step 1} \\ &= \infty && \hbox{since $\lim\limits_{t\to \infty} \ln t = \infty$} \end{align*}\]

Therefore, the improper integral does not exist.

Example 2

Improper integral unbounded on the left

Evaluate \(\displaystyle \int_{-\infty}^{-1} \frac{1}{x^4}~dx\), if it exists.

Step 1: Evaluate \(\displaystyle \int_s^{-1} \frac{1}{x^4} ~dx\).

\[\begin{align*} \int_s^{-1} \frac{1}{x^4} ~dx &= \int_s^{-1} x^{-4} ~dx \\ &= -\frac{1}{3}x^{-3} \Big|_s^{-1} \\ &= -\frac{1}{3}(-1)^{-3} - \left(-\frac{1}{3}s^{-3}\right) \\ &= \frac{1}{3} + \frac{1}{3s^3} && \hbox{simplify} \end{align*}\]

Step 2: Use Step 1 to evaluate \(\displaystyle \int_{-\infty}^{-1} \frac{1}{x^4}~dx\) as the limit of a definite integral.

\[\begin{align*} \int_{-\infty}^{-1} \frac{1}{x^4}~dx &= \lim_{s \rightarrow -\infty} \int_s^{-1} \frac{1}{x^4} ~dx\\ &= \lim_{s \rightarrow -\infty}\left(\frac{1}{3} + \frac{1}{3s^3}\right) && \hbox{using Step 1} \\ &= \frac{1}{3} && \hbox{since $\lim\limits_{s\to -\infty} \frac{1}{3s^3} = 0$} \end{align*}\]

Example 3

Finding the area under a graph unbounded on the right

Find the area of the region under the graph of \(f(x) = e^{-x/2}\) for \(x \geq 2\).

Step 1: Write the area of the region as an improper integral.

\[\text{Area} = \int_{2}^{\infty} e^{-x/2}~dx\]

Step 2: Evaluate \(\displaystyle \int_{2}^{t} e^{-x/2}~dx\).

\[\begin{align*} \int_{2}^{t} e^{-x/2}~dx &= \frac{1}{-1/2}e^{-x/2} \Big|_2^{t} && \hbox{using $\displaystyle \int e^{ax} dx = \frac{1}{a}e^{ax} + C$}\\ &= -2e^{-x/2} \Big|_2^{t} && \hbox{simplify}\\ &= -2e^{-t/2} - (-2e^{-1}) \\ &= 2e^{-1} - 2e^{-t/2} \end{align*}\]

Step 3: Use Step 2 to evaluate \(\displaystyle \int_{2}^{\infty} e^{-x/2}~dx\) as the limit of a definite integral.

\[\begin{align*} \int_{2}^{\infty} e^{-x/2}~dx &= \lim_{t \rightarrow \infty} \int_2^{t} e^{-x/2} ~dx\\ &= \lim_{t \rightarrow \infty}\left(2e^{-1} - 2e^{-t/2}\right) && \hbox{using Step 2} \\ &= 2e^{-1} && \hbox{since $\lim\limits_{t\to \infty} e^{-t/2} = 0$} \end{align*}\]

Therefore, the area of the region is \(2/e\).

Improper Integrals over \((-\infty, \infty)\)

Definition

Let \(f\) be a continuous function on \((-\infty,\infty)\). Let \(c\) be a real number, and suppose that the improper integrals

\[\int_{\infty}^c f(x)~dx ~~~~\text{ and }~~~~ \int_c^\infty f(x)~dx \]

both exist. Then the improper integral of \(f\) over \((-\infty, \infty)\) is defined by

\[\begin{align*} \int_{-\infty}^\infty f(x)~dx &= \int_{-\infty}^c f(x)~dx + \int_c^\infty f(x)~dx \\ &= \lim_{s \rightarrow -\infty} \int_s^c f(x)~dx + \lim_{t \rightarrow \infty} \int_c^t f(x)~dx. \end{align*}\]

If the liits exist, the value of the above improper integral is the same regardless of the value we choose for \(c\) and therefore the value \(c=0\) is typically used.

Geometric Interpretation of an Improper Integral

If the above improper integral exists, it corresponds to the area of a region that is unbounded on the left and on the right.

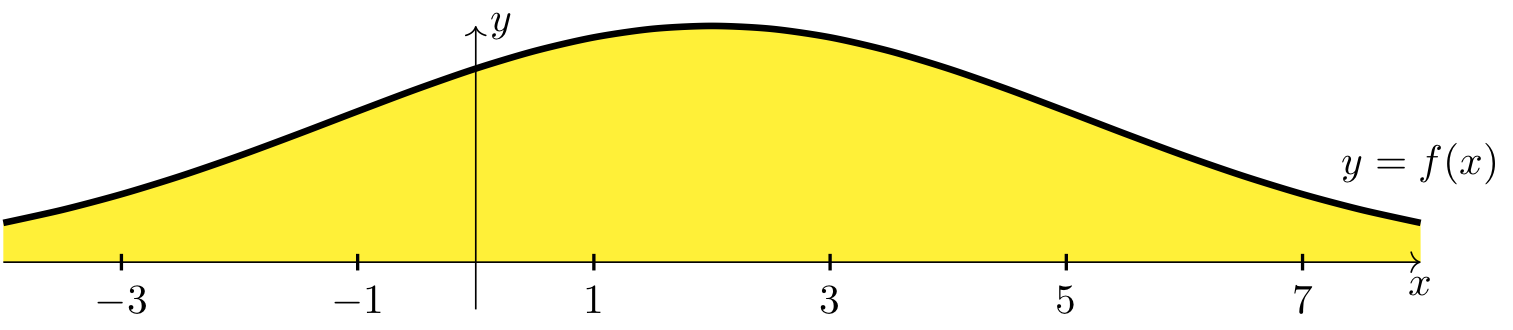
Fig. 17 Improper integral unbounded on the left and the right

Long Text Description

There is a horizontal x axis with the points -3, -1, 1, 3, 5, and 7 labeled. There is a vertical y axis. The curve y=f(x), which is increasing and concave up as it comes in from the left, becomes increasing and concave down, becomes decreasing and concave down, and then becomes decreasing and concave up as it goes off to the right, is plotted. The entire region between the curve y= f(x) and the x axis is shaded yellow.

Example 4

Improper integral unbounded on both sides

Evaluate \(\displaystyle \int_{-\infty}^\infty \frac{e^x}{(1 + e^x)^3}~dx\), if it exists.

Step 1: Rewrite the integral as a sum of two improper integrals.

\[ \int_{-\infty}^\infty \frac{e^x}{(1 + e^x)^3}~dx = \int_{-\infty}^0 \frac{e^x}{(1 + e^x)^3}~dx + \int_{0}^\infty \frac{e^x}{(1 + e^x)^3}~dx.\]

Step 2: Compute \(\displaystyle \int \frac{e^x}{(1+e^{x})^3} ~dx\).

Using the following substitution

\[u = 1+e^x \qquad du = e^x~dx\]

gives

\[\begin{align*} \int \frac{e^x}{(1+e^{x})^3} ~dx &= \int \left(1+e^{x}\right)^{-3}e^x~dx \\ &= \int u^{-3}~du\\ &= -\frac{1}{2}u^{-2}+C\\ &= -\frac{1}{2(1+e^x)^2} + C \end{align*}\]

Step 3: Evaluate \(\displaystyle \int_{-\infty}^0 \frac{e^x}{(1 + e^x)^3}~dx\).

\[\begin{align*} \int_{-\infty}^0 \frac{e^x}{(1 + e^x)^3}~dx &= \lim_{s\rightarrow -\infty} \int_s^0 \frac{e^x}{(1 + e^x)^3}~dx \\ &= \lim_{s\rightarrow -\infty} -\frac{1}{2(1+e^x)^2}\Biggr|_s^0 && \hbox{using Step 2} \\ &= \lim_{s\rightarrow -\infty} -\frac{1}{2(1+e^0)^2} - \left(-\frac{1}{2(1+e^s)^2}\right) \\ &= \lim_{s\rightarrow -\infty} -\frac{1}{8} + \frac{1}{2(1+e^s)^2} && \hbox{since $e^0 = 1$} \\ &= -\frac{1}{8} + \frac{1}{2} && \hbox{since $\lim\limits_{s\to -\infty} e^s = 0$}\\ &= \frac{3}{8} \end{align*}\]

Step 4: Evaluate \(\displaystyle \int_0^{\infty} \frac{e^x}{(1 + e^x)^3}~dx\).

\[\begin{align*} \int_0^\infty \frac{e^x}{(1 + e^x)^3}~dx &= \lim_{t\rightarrow \infty} \int_0^t \frac{e^x}{(1 + e^x)^3}~dx \\ &= \lim_{t\rightarrow \infty} -\frac{1}{2(1+e^x)^2}\Biggr|_0^t && \hbox{using Step 2} \\ &= \lim_{t\rightarrow \infty} -\frac{1}{2(1+e^t)^2} - \left(-\frac{1}{2(1+e^0)^2}\right) \\ &= \lim_{t\rightarrow \infty} -\frac{1}{2(1+e^t)^2} + \frac{1}{8} && \hbox{since $e^0=1$}\\ &= 0 + \frac{1}{8} && \hbox{since $\lim\limits_{t\to \infty} e^t = \infty$}\\ &= \frac{1}{8} \end{align*}\]

Step 5: Evaluate \(\displaystyle \int_{-\infty}^{\infty} \frac{e^x}{(1 + e^x)^3}~dx\).

\[\begin{align*} \int^\infty_{-\infty} \frac{e^x}{(1+e^x)^3}~dx &= \int_{{-\infty}}^0 \frac{e^x}{(1 + e^x)^3}~dx + \int_{0}^\infty \frac{e^x}{(1 + e^x)^3}~dx && \hbox{using Step 1}\\ \\ &= \frac{3}{8} + \frac{1}{8} && \hbox{using Steps 3 and 4}\\ \\ &= \frac{1}{2} \end{align*}\]

Example 5

Improper integral unbounded on both sides

Evaluate \(\displaystyle \int_{-\infty}^\infty xe^{-x^2}~dx\), if it exists.

Step 1: Compute \(\displaystyle \int xe^{-x^2} ~dx\).

Using the following substitution

\[u = -x^2 \qquad du = -2x ~dx ~~~~ \hbox{(or $-\frac{1}{2}~du = x ~dx$)}\]

gives

\[\begin{align*} \int xe^{-x^2} ~dx &= \int -\frac{1}{2}e^u ~dx \\ &= -\frac{1}{2}e^u + C\\ &= -\frac{1}{2}e^{-x^2} + C \end{align*}\]

Step 2: Evaluate \(\displaystyle \int_{-\infty}^0 xe^{-x^2}~dx\).

\[\begin{align*} \int_{-\infty}^0 xe^{-x^2} ~dx &= \lim_{s\rightarrow -\infty} \int_s^0 xe^{-x^2} ~dx \\ &= \lim_{s\rightarrow -\infty} -\frac{1}{2} e^{-x^2} \Big|_s^0 && \hbox{using Step 1}\\ &= \lim_{s\rightarrow -\infty} -\frac{1}{2}e^{0} - \left(-\frac{1}{2}e^{-s^2} \right) \\ &= \lim_{s\rightarrow -\infty} -\frac{1}{2} + \frac{1}{2}e^{-s^2} && \hbox{since $e^0=1$} \\ &= -\frac{1}{2} && \hbox{since $\lim\limits_{s\to-\infty} e^{-s^2} = 0$} \end{align*}\]

Step 3: Evaluate \(\displaystyle \int_0^{\infty} xe^{-x^2}~dx\).

\[\begin{align*} \int_0^{\infty} xe^{-x^2} ~dx &= \lim_{t\rightarrow \infty} \int_0^t xe^{-x^2} dx \\ &= \lim_{t\rightarrow \infty} -\frac{1}{2} e^{-x^2} \Big|_0^t && \hbox{using Step 1}\\ &= \lim_{t\rightarrow \infty} -\frac{1}{2}e^{-t^2} - \left(-\frac{1}{2}e^{0} \right) \\ &= \lim_{t\rightarrow \infty} -\frac{1}{2}e^{-t^2} + \frac{1}{2} \\ &= \frac{1}{2} && \hbox{since $\lim\limits_{t\to\infty} e^{-t^2} = 0$} \end{align*}\]

Step 4: Evaluate \(\displaystyle \int_{-\infty}^{\infty} xe^{-x^2}~dx\).

\[\begin{align*} \int^\infty_{-\infty} xe^{-x^2} ~dx &= \int_{{-\infty}}^0 xe^{-x^2}dx + \int_{0}^\infty xe^{-x^2}dx \\ &= -\frac{1}{2} + \frac{1}{2} && \hbox{using Steps 2 and 3}\\ &= 0 \end{align*}\]