Limits at Infinity#
Definition
The limit of \(f(x)\) as \(x\) approaches (positive) infinity is equal to the finite number \(L\), denoted by
if \(f(x)\) can be made as close to \(L\) as we want by taking \(x\) large enough.
Similarly, the limit of \(f(x)\) as \(x\) approaches negative infinity is equal to the finite number \(M\), denoted by
if \(f(x)\) can be made as close to \(M\) as we want by taking \(x\) to be negative and sufficiently large in absolute value.
Example 1#
The following graph illustrates a function \(f(x)\) that approaches a value of 400 as \(x\) increases without bound. In other words,
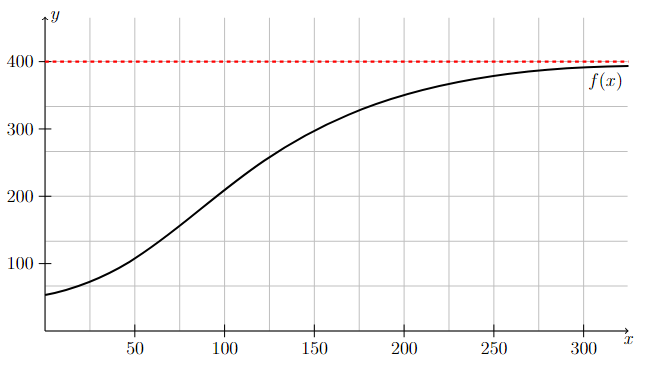
Long Text Description
There is a horizontal x-axis with the points 50, 100, 150, 200, 250, and 300 marked. There is a vertical y-axis with the points 100, 200, 300, and 400. There is a horizontal red dotted line at y = 400. The graph of a function is plotted on these axes. The function is increasing and approaches the horizontal dotted line from below, but never reaches it. The closer the graph of the function gets to the horizontal dotted line, the slower the graph of the function increases.
Properties of Limits at Infinity#
All previous properties for limits apply when \(a\) is replaced with \(\infty\) or \(-\infty\). Furthermore, the following additional properties are especially useful when evaluating limits at infinity. For all \(n>0\), we have
\(\lim\limits_{x \to \infty} \dfrac{1}{x^n}=0 \)
\(\lim\limits_{x \to -\infty} \dfrac{1}{x^n}=0\), provided that \(x^n\) is defined for \(x<0\).
Example 2#
Notice how the graph of \(y=1/x\) approaches the \(x\)-axis as \(x\) approaches positive and negative infinity. In other words,
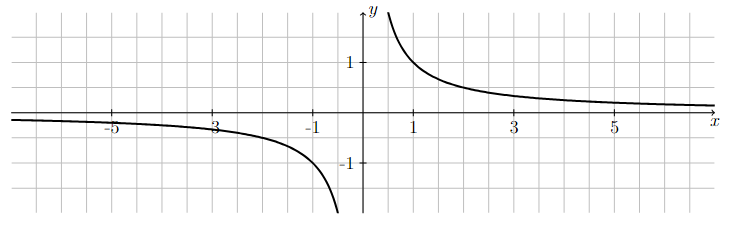
Long Text Description
There is a horizontal x-axis with the points -5, -3, -1, 1, 3, and 5 marked. There is a vertical y-axis with the points -1 and 1 marked. The graph of the function y = 1/x is plotted on these axes. This function comes in just below the x-axis from the left, decreases to negative infinity as x approaches zero from the left. The function is not defined at x = 0. As x increases past zero, the function comes down from positive infinity and decreases towards the x-axis as it continues to the right.
Example 3#
Notice how the graph of \(y=1/\sqrt{x}\) approaches the \(x\)-axis as \(x\) approaches positive infinity. In other words,
Furthermore, there is no discussion of the limit as \(x\) approaches negative infinity since \(\sqrt{x}\) is not defined for negative values of \(x\).
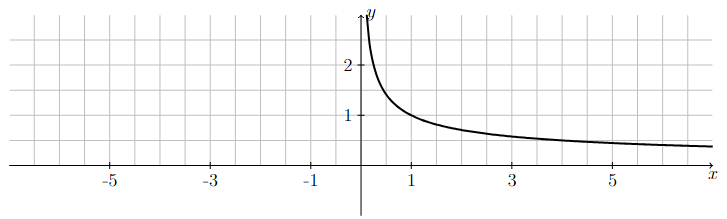
Long Text Description
There is a horizontal x-axis with the points -5, -3, -1, 1, 3, and 5 marked. There is a vertical y-axis with the points 1 and 2 marked. The graph of the function one over square root x is plotted on these axes. The graph does not appear above negative x values. The function is not defined at x = 0. As x increases past zero, the function comes down from positive infinity and decreases towards the x-axis as it continues to the right.
Limits at Infinity of Rational Functions#
For Rational Functions, a limit at infinity, whether it be \(\displaystyle\lim_{x\to\infty}\) or \(\displaystyle\lim_{x\to -\infty}\), can be determined by comparing the degree of the polynomial in the numerator to the degree of the polynomial in the denominator.
For infinite limits of Rational Functions, if the
highest power is in the denominator, then the limit will equal \(0\)
highest power is in the numerator, then the limit will equal \(\pm\infty\) (DNE)
highest power is the same in both the numerator and denominator, then the limit will equal the ratio of the leading coefficients, i.e. the ratio of the coefficients in front of the highest powers in the numerator and the denominator.
Example 4#
Applying the guidelines:
\(\displaystyle\lim_{x\to\infty}\frac{x+3}{6x^2+3x+1}\) = 0 (highest power is in denominator)
\(\displaystyle\lim_{x\to-\infty}\frac{6x^{3}+3}{x^{2}+4x-7}\) = \(-\infty\) or DNE (highest power is in numerator)
\(\displaystyle\lim_{x\to\infty}\frac{4x^5+3x-8}{9x^5-6x^3}\) = \(4/9\) (highest powers are the same)