Try It Yourself#
Exercise 1#
Simplify
Rewrite \(\dfrac{3}{x-1} - \dfrac{5}{2x+1}\) as a single ratio.
Show answer
Answer: \(\dfrac{x+8}{(x-1)(2x+1)}\)
Exercise 2#
Expand
Expand \((8x+11)(2x-5)\) using the FOIL method.
Show answer
Answer: \(16x^2 - 18x - 55\)
Exercise 3#
Expand
Expand \(5x^6(3x-4)^2\).
Show answer
Answer: \(45x^8 - 120x^7 + 80x^6\)
Exercise 4#
Expand
Expand \((1+3x)(1-3x)(2+x)\).
Show answer
Answer: \(2 + x - 18x^2 - 9x^3\)
Exercise 5#
Factor
Factor \(4x^5 - 25x^3\).
Show answer
Answer: \(x^3(2x-5)(2x+5)\) (use difference of squares)
Exercise 6#
Simplify
Simplify
by factoring both the numerator and the denominator. Assume that \(x\neq 0\) and \(x\neq 3\).
Show answer
Answer: \(-2(x+2)/(x+3)\)
Exercise 7#
Factor and Simplify
Factor and simplify \(10x(x+2)^5 - 5x^2(x+2)^3\).
Show answer
Answer: \(5x(x+2)^3(2x^2+7x + 8)\)
Exercise 8#
Sketch a line
Sketch the graph of the line defined by \(y = \dfrac{1}{4}(x-5) - 2\). Use the fact that the line is described in point-slope form.
Long Text Description
There is a horizontal x-axis with the points -4, 4, 8, 12, and 16 marked. There is a vertical y-axis with the points -4, -2, and 2 marked. There is a grey grid of one unit by one unit cells in the background.
Show answer
Answer: Line through the point \((5,-2)\) with a slope of \(1/4\). The line has an \(x\)-intercept at \(x=13\) and a \(y\)-intercept at \(y=-3.25\)
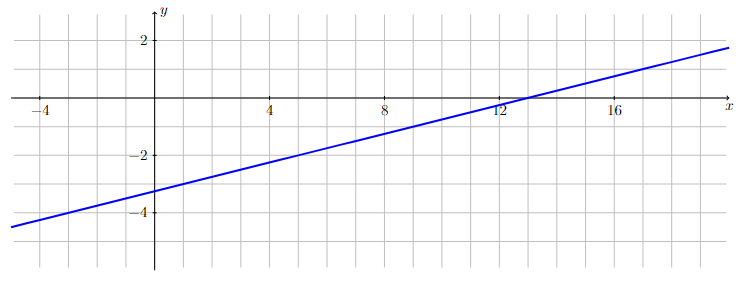
Long Text Description
Graph of the line y = (x-5)/4 - 2. The line crosses the y-axis at the point (0,-3.25) and crosses the x-axis at the point (13,0).
Exercise 9#
Solve an inequality
Find all values of \(x\) such that \(x^2 - 16 > 0\). Write your answer using interval notation.
Show answer
Answer: \((-\infty,-4) \cup (4,\infty)\)
Exercise 10#
Sketch a line
Sketch the graph of \(f(x) = 12x^2 - x - 6\) by finding the \(x\) and \(y\)-intercepts (see Graphing, Example 6).
Long Text Description
There is a horizontal x-axis with the points -1 and 1 marked. There is a vertical y-axis with the points -8, -6, -4, -2, 2, 4, and 6 marked. There is a grey grid of one quarter unit by one unit cells in the background.
Show answer
Answer: Parabola that opens upward and goes through the points \((0,-6)\), \((3/4,0)\), and \((-2/3,0)\).
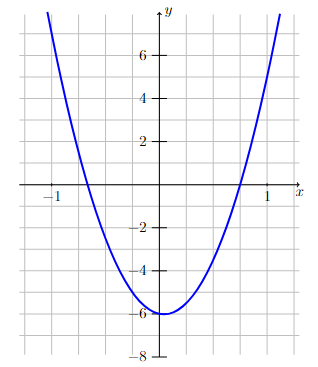
Long Text Description
The graph of the function y = 12 x squared - x - 6. The graph is a parabola that opens up, crosses the x-axis at the points (-2/3,0) and (3/4,0), and crosses the y-axis at the point (0,-6).
Exercise 11#
Domain
Determine the domain of each of the following functions. Write your answer using interval notation.
\(g(x) = \dfrac{x}{12x^2 - x - 6}\)
\(h(x) = \dfrac{x}{\sqrt{12x^2 - x - 6}}\)
Show answer
Answer: 1.) \((-\infty,-2/3) \cup (-2/3,3/4) \cup (3/4,\infty)\),
2.) \((-\infty,-2/3) \cup (3/4,\infty)\)
