Intervals of Concavity#
Definitions#
Definition
A function is concave up on an interval if its derivative is increasing on the interval.
The graph of a function that is concave up on an interval will resemble a portion of a parabola that opens up on that interval.
Definition
A function is concave down on an interval if its derivative is decreasing on the interval.
The graph of a function that is concave down on an interval will resemble a portion of a parabola that opens down on that interval.
What the Sign of \(f''\) Tells Us About \(f\).
If \(f''(x) > 0\) for all \(x\) on the interval \((a,b)\), then \(f\) is concave up on \((a,b)\).
If \(f''(x) < 0\) for all \(x\) on the interval \((a,b)\), then \(f\) is concave down on \((a,b)\).
Example 1#
Finding intervals of concavity from the graph of a function
The following is the graph of a continuous function that is concave down on the interval \((1,4)\) and concave up on the interval \((4,7)\).
Notice how the graph resembles a parabola that opens down on the interval \((1,4)\) and resembles a parabola that opens up on the interval \((4,7)\).
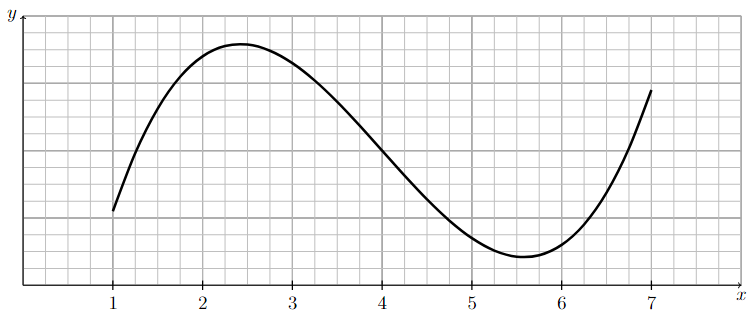
Long Text Description
There is a horizontal x-axis with the points 1, 2, 3, 4, 5, 6, and 7 marked. There is a vertical y-axis. The graph of a function is plotted on these axes. Reading from left to right, the function goes up at a slowing pace, reaches a rounded corner, decreases at an accelerating pace, decreases at a slowing pace, reaches another rounded corner, and goes upward at an accelerating pace.
Example 2#
Finding intervals of concavity using the graph of the derivative
The following graph corresponds to \(f'(x)\), the first derivative of \(f(x)\).
Using the graph of \(f'(x)\), determine the intervals of concavity of \(f(x)\). You may assume that \(f'(x)\) is continuous for all \(x\) and that \(f'(x)\) has relative extrema only at \(x = -1\), \(x = 1\), and \(x = 4\).
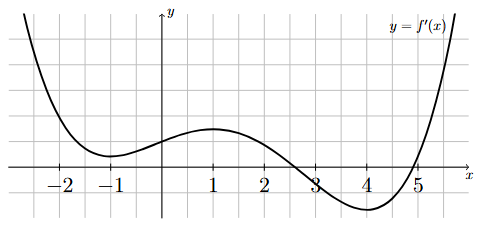
Long Text Description
There is a horizontal x-axis with the points -2, -1, 1, 2, 3, 4 and 5 marked. There is a vertical y-axis with no points marked. The graph of a continuous function is plotted here. The function is decreasing for x < -1, increasing for -1 < x < 1, decreasing for 1 < x < 4, and increasing for x > 4.
Step 1: Use the graph to determine the intervals of increase/decrease of \(f'\).
Since we were given that the only relative extrema of \(f'\) are at \(x = -1\), \(x = 1\), and \(x = 4\), we can assume these are the only places where the increasing/decreasing behavior of \(f'\) changes. In other words, we only have to determine the behavior of \(f'\) on each of the following intervals:
Using the given graph of the first derivative, we have that
\(f'\) is decreasing on \((-\infty,-1)\),
\(f'\) is increasing on \((-1,1)\),
\(f'\) is decreasing on \((1,4)\), and
\(f'\) is increasing on \((4,\infty)\).
Step 2: Determine the intervals of concavity of \(f\).
Recall that \(f\) is concave up on intervals where \(f'\) is increasing and concave down on intervals where \(f'\) is decreasing.
Therefore, \(f\) is concave up on \((-1,1) \cup (4,\infty)\) and concave down on \((-\infty,-1) \cup (1,4)\).
Finding Intervals of Concavity using the Second Derivative#
How to Find Intervals of Concavity of a Function
Find all values of \(x\) such that \(f''(x) = 0\) or \(f''(x)\) does not exist.
Break up domain of \(f\) into open intervals between values found in Step 1.
Evaluate \(f''(x)\) at one value, \(c\), from each interval, \((a,b)\), found in Step 2.
If \(f''(c) > 0\), then \(f\) is concave up on \((a,b)\).
If \(f''(c) < 0\), then \(f\) is concave down on \((a,b)\).
Example 3#
Finding intervals of concavity using the graph of the second derivative
The following graph corresponds to \(f''(x)\), the second derivative of \(f(x)\).
Using the graph of \(f''(x)\), determine the intervals of concavity of \(f(x)\). You may assume that \(f''(x)\) is continuous for all \(x\) and \(f''(x) = 0\) only when \(x = -2\) and \(x = 1\).
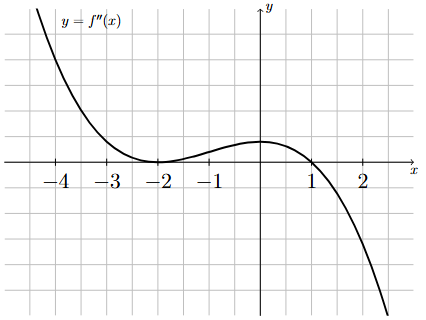
Long Text Description
There is a horizontal x-axis with the points -4, -3, -2, -1, 1, and 2 marked. There is a vertical y-axis with no points marked. The graph of a continuous function is plotted here. The graph of the function touches the x-axis at x = -2 and at x = 1. The graph is above the x-axis for x < - 2 and for -2 < x < 1. The graph is below the x-axis for x > 1.
Step 1: Find all values of \(x\) such that \(f''(x) = 0\).
We were given that \(f''(x) = 0\) only when \(x = -2\) and when \(x = 1\).
Step 2: Find all values of \(x\) such that \(f''(x)\) does not exist.
Notice that \(f''(x)\) is defined for all real numbers since we were told that \(f''(x)\) is continuous for all \(x\).
Step 3: Break up the domain of \(f\) into subintervals.
Break up the domain of \(f\) into subintervals based on the values found in Steps 1 and 2.
Since we found \(x=-2\) and \(x=1\) to be the only values where \(f''(x) = 0\) or where \(f''(x)\) is not defined, we break up the domain of \(f\) (which is \((-\infty,\infty)\)) into the following subintervals:
Step 4: Use the graph to determine the sign of \(f''(x)\) on each interval.
\(\mathbf{(-\infty,-2)}\): Since the graph of \(f''(x)\) is above the \(x\)-axis on this interval, \(f''(x) > 0\) for all \(x\) on \((-\infty,-2)\).
\(\mathbf{(-2,1)}\): Since the graph of \(f''(x)\) is above the \(x\)-axis on this interval, \(f''(x) > 0\) for all \(x\) on \((-2,1)\).
\(\mathbf{(1,\infty)}\): Since the graph of \(f''(x)\) is below the \(x\)-axis on this interval, \(f''(x) < 0\) for all \(x\) on \((1,\infty)\).
Step 5: Use the sign of \(f''\) to determine the intervals of concavity of \(f\) .
Recall that \(f(x)\) is concave up on intervals where \(f''(x) > 0\) and concave down on intervals where \(f''(x) < 0\).
Therefore, \(f(x)\) is concave up on \((-\infty,-2) \cup (-2,1)\) and concave down on \((1,\infty)\).
Example 4#
Finding intervals of concavity
If the second derivative of \(f(x)\) is
find the intervals of concavity of \(f\).
Step 1: Find all values of \(x\) such that \(f''(x) = 0\).
which equals zero when \(x=0\) and \(x=4\).
Step 2: Find all values of \(x\) such that \(f''(x)\) does not exist.
\(f''(x)\) does not exist when \(x=6\).
Step 3: Perform an interval sign analysis for \(f''\).
Break up the domain of \(f\) at each value found in Steps 1 and 2. Plug one number from each subinterval into \(f''(x)\) to determine the sign of \(f''(x)\) on each interval.

Fig. 7 Interval analysis of \(f''(x) = \frac{x(x-4)}{x-6}\).#
Long Text Description
A number line with positive and negative signs assigned to intervals, which are negative to the left of zero, positive from zero to four, negative from four to six, and positive to the right of six.
Therefore, \(f\) is concave up on the intervals \((0,4)\) and \((6,\infty)\) and concave down on the intervals \((-\infty,0)\) and \((4,6)\).
