An Application

An Application#

The cost of construction

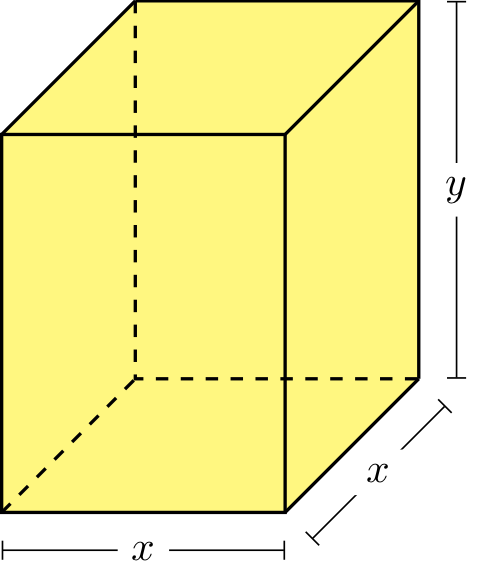
A rectangular box with a square base and a volume of \(24\) ft\(^3\) has costs to construct of \(\$10 / \text{ft}^2\) for the sides, \(\$20 / \text{ft}^2\) for the top, and \(\$40 / \text{ft}^2\) for the base. If \(x\) denotes the length of one side of the base (in feet), determine the function in the variable \(x\) giving the total cost of constructing the box in dollars and state the appropriate domain

Step 1:   Draw and label a figure.
a box with base length and depth $x$ and height $y$
Long Text Description

A two dimensional projective diagram of a three dimensional square prism, with the square face horizontal and of side length x, and height y.

Note that we are temporarily using the variable \(y\) to denote the height of the box.

Step 2:   Translate the problem description into a function.

Translate the problem description into a function of the variables \(x\) and \(y\).

\[\begin{eqnarray*} \text{Cost} &=& 40\cdot\text{(area of base)} + 10\cdot\text{(area of sides)} + 20\cdot\text{(area of top)} \\ &=& 40x^2 + 10\cdot4xy + 20\cdot x^2 \\ &=& 60x^2 + 40xy \end{eqnarray*}\]
Step 3:   Write the total cost as a function of one variable.

Use the conditions given in the problem to write the total cost as a function of one variable.

Since the volume of the box is given to be \(24\) ft\(^3\), the variables \(x\) and \(y\) must satisfy the following equation.

\[x^2y = 24\]

Solving for \(y\) yields \(y = 24/x^2\). Substituting this into our formula for cost in Step 2, we obtain \(C(x)\), the cost of constructing the box as a function of \(x\).

\[\begin{eqnarray*} C(x) &=& 60x^2 + 40x\left(\frac{24}{x^2}\right) \\ &=& 60x^2 + \frac{960}{x} \end{eqnarray*}\]
Step 4:   Determine the appropriate domain.

Note any restrictions to be placed on the domain of the function from physical considerations of the problem.

Since \(x\) denotes the length of one side of the base, its value must be at least zero. However, \(x\) cannot be equal to zero since the height, \(y = 24/x^2\), is undefined at \(x=0\). Therefore, the domain of \(C(x)\) is \((0,\infty)\).