Asymptotes

Definitions

Definition

The line \(x=a\) is a vertical asymptote of the function \(f\) if

\[\lim_{x \to a^+} f(x)= \pm \infty \qquad \text{or} \qquad \lim_{x \to a^-} f(x)= \pm \infty\]

Vertical Asymptotes of a Rational Function

The rational function

\[f(x) = \dfrac{g(x)}{h(x)}\]

has a vertical asymptote at \(x=a\) if \(h(a) = 0\) and \(g(a) \neq 0\).

We can find the vertical asymptotes by factoring \(g(x)\) and \(h(x)\) and then cancelling common factors. Any value of \(x\) that makes the denominator equal to zero, after cancellation, corresponds to a vertical asymptote.

Definition

The line \(y=b\) is a horizontal asymptote of the function \(f\) if:

\[\lim_{x \to \infty} f(x)= b \qquad \text{or} \qquad \lim_{x \to -\infty} f(x)= b\]

Horizontal asymptotes describe the behavior of the graph of \(f\) for large positive and large negative values of \(x\). The graph of \(f\) should approach the horizontal asymptote for large values of \(x\).

A function can have at most two different horizontal asymptotes.

Horizontal Asymptotes of a Rational Function

Horizontal asymptotes of rational functions are determined by computing the limit at infinity of the given rational function, which can be accomplished by comparing the degree of the numerator to the degree of the denominator. See Limits at Infinity of Rational Functions for a review of this process.

Example 1

Graph of vertical and horizontal asymptotes

The following graph is an example of a function that has vertical asymptotes at \(x=-1\) and \(x=3\) and a horizontal asymptote at \(y=1\).

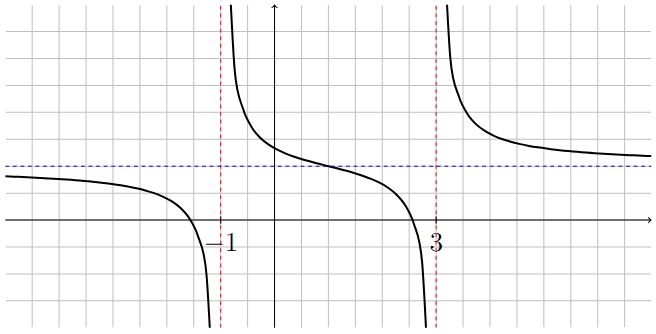
Long Text Description

There is a horizontal x-axis with the points -1 and 3 marked. There is a vertical y-axis. There is a grid in the background of 1/2 by 1/2 squares. There is a blue dashed horizontal line at y = 1. There is a red dashed vertical line at x = -1. There is a red dashed vertical line at x = 3. The graph of a function is plotted on these axes. From left to right, the function decreases from the blue dashed line and goes to negative infinity as it approaches the red dashed line at x = -1, comes down from positive infinity to the right of -1, goes down to negative infinity as it approaches the red dashed line at x = 3, and comes down from positive infinity at x = 3 towards the blue dashed line as it heads off to the right.

Example 2

Find asymptotes

Find the horizontal and vertical asymptotes of \(f(x)=\dfrac{7x^2+2x+1}{2x^2+3x-9}\).

Step 1:   Horizontal Asymptotes.

Since the degree of the numerator and the denominator are the same, both limits at infinity are equal to the ratio of leading coefficients.

\[\lim_{x\to -\infty} f(x) = \frac{7}{2} = \lim_{x\to \infty} f(x)\]

Therefore, \(y=7/2\) is the only horizontal asymptote of \(f\).

Step 2:   Vertical Asymptotes.

Factor and simplify \(f(x)\).

\[\begin{align*} f(x) &= \frac{7x^2+2x+1}{2x^2+3x-9} \\ &= \frac{7x^2+2x+1}{(2x-3)(x+3)} && \text{AC grouping} \end{align*}\]

Therefore \(x =-3\) and \(x=3/2\) are possible vertical asymptotes.

Since the numerator cannot be factored, to make sure these values of \(x\) correspond to vertical asymptotes, plug them into the numerator, \(g(x) = 7x^2+2x+1\), and see if they also make the numerator equal to zero.

Since \(g(-3) \neq 0 \) and \(g(3/2) \neq 0\), \(x=-3\) and \(x=3/2\) are both vertical asymptotes.

Example 3

Find asymptotes

Find the horizontal and vertical asymptotes of \(f(x)=\dfrac{x^4-x^2}{x^3 + x^2 - 2 x}\).

Step 1:   Horizontal Asymptotes.

Since the degree of the numerator, \(4\), is larger than the degree of the denominator, \(3\), both limits at infinity do not exist.

\[\lim_{x\to -\infty} f(x) = -\infty \qquad \lim_{x\to \infty} f(x) = \infty\]

Therefore, \(f\) does not have any horizontal asymptotes.

Step 2:   Vertical Asymptotes.

Factor and simplify \(f(x)\).

\[\begin{align*} f(x) &= \frac{x^2(x^2-1)}{x(x^2 + x - 2)} && \text{pull out common factors}\\ &= \frac{x^2(x-1)(x+1)}{x(x+2)(x-1)} && \text{factor numerator and denominator}\\ &= \frac{x^{\cancel{2}}\cancel{(x-1)}(x+1)}{\cancel{x}(x+2)\cancel{(x-1)}} && \text{cancel common factors}\\ &= \frac{x(x+1)}{x+2} \end{align*}\]

Since only \(x=-2\) makes the denominator equal to zero, after cancellation, \(x=-2\) is the only vertical asymptote.