Absolute Extrema

Definitions

Definition

A function \(f\) has an absolute maximum at \(x=c\) if \(f(c) \geq f(x)\) for all \(x\) in the domain of \(f\). In this case, \(f(c)\) is called the absolute maximum value of \(f\).

Definition

A function \(f\) has an absolute minimum at \(x=c\) if \(f(c) \leq f(x)\) for all \(x\) in the domain of \(f\). In this case, \(f(c)\) is called the absolute minimum value of \(f\).

Absolute Extrema on a Closed Interval

If a function \(f\) is continuous on a closed interval \([a,b]\), then \(f\) has both an absolute maximum value and an absolute minimum value on \([a,b]\).

Example 1

Absolute extrema

For a continuous function defined on a closed interval, absolute extrema can either appear at the endpoints of the interval or at the same place as a relative extrema.

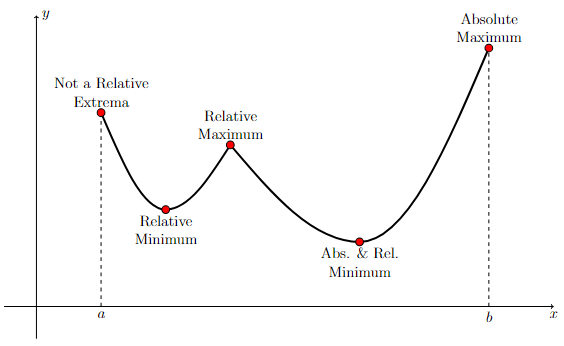
Long Text Descriptions

There is a horizontal x axis with the points a and b marked. There is a vertical y axis. The graph of a function is plotted on these axes. The function begins on the left with a red marked point labelled “not a relative extremum,” is decreasing and concave up until it hits a rounded corner at a red marked point labelled “relative minimum,” is increasing and concave up until it hits a hard corner marked red and labelled “relative maximum,” decreases while concave up to a rounded corner at a red marked point labelled “absolute and relative maximum,” and increases and is concave up until it ends at a point labelled “absolute maximum.” There is a vertical dashed line between the point labelled “not a relative extremum” and the point (a,0). There is a vertical dashed line between the point labelled “absolute maximum” and the point (b,0).

How to Find the Absolute Extrema of a Function on a Closed Interval

Finding Absolute Extrema on a Closed Interval

To find the absolute extrema of a function \(f\) on a closed interval \([a,b]\)

1. Find the critical points of \(f\) that lie on \((a,b)\).

2. Compute the value of \(f\) at each critical point found in Step 1 and compute \(f(a)\) and \(f(b)\).

3. The absolute maximum value and absolute minimum value of \(f\) will correspond to the largest and smallest numbers, respectively, found in Step 2.

Example 2

Finding absolute extrema

Find the absolute extrema of the function \(f(x)=x^3-2x^2-4x+4\) on the interval \([0,3]\).

Step 1: Decide whether \(f\) is continuous on the interval.

Observe that \(f\) is continuous on the closed interval \([0,3]\).

Step 2: Find the critical points of \(f\) on \((0,3)\), if any.

\[\begin{align*} f'(x) &= 3x^2-4x-4\\ &=(3x+2)(x-2) \end{align*}\]

Therefore, \(f'(x)=0\) when \(x=-2/3\) and \(x=2\). But since \(x=-2/3\) is not on the interval \((0,3)\), \(x=2\) is the only critical point on \((0,3)\).

Step 3: Evaluate \(f(x)\) at critical points on \((0,3)\) and the endpoints of \([0,3]\).

\[\begin{align*} f(0) &= 4 \\ f(2) &= -4 \\ f(3) &= 1 \end{align*}\]

Step 4: Find absolute extrema by comparing values from Step 3.

It follows that \(f(2)=-4\) is the absolute minimum value and \(f(0)=4\) is the absolute maximum value.

Example 3

Finding absolute extrema

Find the absolute extrema of the function \(f(x)=4x^5+5x^4\) on the interval \([-2,1]\).

Step 1: Decide whether \(f\) is continuous on the interval.

Observe that \(f\) is continuous on the closed interval \([-2,1]\).

Step 2: Find the critical points of \(f\) on \((-2,1)\), if any.

\[\begin{align*} f'(x) &= 20x^4+20x^3\\ &=20x^3(x+1) \end{align*}\]

Therefore, \(f'(x) = 0\) when \(x=0\) and \(x=-1\), both of which are on \((-2,1)\).

Step 3: Evaluate \(f(x)\) at critical points on \((-2,1)\) and the endpoints of \([-2,1]\).

\[\begin{align*} f(-2) &= -48 \\ f(-1) &= 1 \\ f(0) &= 0 \\ f(1) &= 9 \end{align*}\]

Step 4: Find absolute extrema by comparing values from Step 3.

It follows that \(f(-2)=-48\) is the absolute minimum value and \(f(1)=9\) is the absolute maximum value.

Example 4

Finding absolute extrema

Find the absolute extrema of the function \(f(x)=\dfrac{1}{x-1}\) on the interval \([2,4]\).

Step 1: Decide whether \(f\) is continuous on the interval.

Observe that \(f\) has a discontinuity at \(x=1\), however this is not on the interval \([2,4]\). Therefore \(f\) is continuous on the closed interval \([2,4]\).

Step 2: Find the critical points of \(f\) on \((2,4)\), if any.

\[\begin{align*} f'(x) &= \frac{d}{dx} (x-1)^{-1} \\ &= -(x-1)^{-2}\\ &= -\frac{1}{(x-1)^2} \end{align*}\]

which is never equal to zero, but does always exist on the interval \((2,4)\). Notice that \(x=1\) is not a critical point of \(f\) since \(f(1)\) is not defined. In other words, \(f\) does not have any critical points.

Step 3: Evaluate \(f(x)\) at critical points on \((2,4)\) and the endpoints of \([2,4]\).

Since there are no critical points, we need only evaluate \(f\) at \(x=2\) and \(x=4\).

\[\begin{align*} f(2) &= 1 \\ f(4) &= 1/3 \end{align*}\]

Step 4: Find absolute extrema by comparing values from Step 3.

It follows that \(f(4)=1/3\) is the absolute minimum value and \(f(2)=1\) is the absolute maximum value.