The Concept of the Derivative

Definitions

Definition

The average rate of change of \(f(x)\) over the interval \([a, a+h]\), which is also the slope of the line secant to the graph of \(f(x)\) through the points \((a,f(a))\) and \((a+h, f(a+h))\), is given by

\[ \frac{f(a+h) - f(a)}{h}.\]

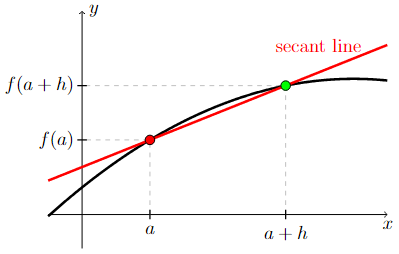
Long Text Description

There is a horizontal x-axis with points a and a+h marked. There is a vertical y-axis with the points f(a) and f(a+h) marked. The graph of a generic function is drawn. The point (a,f(a)) is marked by a red dot on the graph of the function. The point (a+h, f(a+h)) is marked by a green dot on the graph of the function. A red line is drawn through the points (a,f(a)) and (a+h,f(a+h)) and is labeled as the secant line.

Definition

The instantaneous rate of change of \(f(x)\) at \(x=a\), which is also the slope of the line tangent to the graph of \(f(x)\) at \((a,f(a))\), is given by

\[\lim_{h\to 0} \frac{f(a+h) - f(a)}{h},\]

if the limit exists.

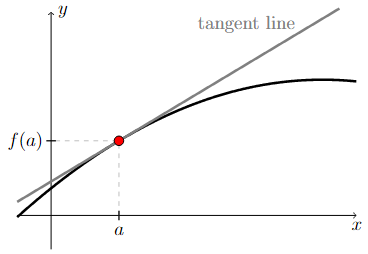
Long Text Description

There is a horizontal x-axis with point a marked. There is a vertical y-axis with the point f(a) marked. The graph of a generic function is drawn. The point (a,f(a)) is marked by a red dot on the graph of the function. A gray line is drawn through the point (a,f(a)) and is labeled as the tangent line. The tangent line is drawn so that it closely resembles the graph of the function near the point (a,f(a)).

The Limit Definition of the Derivative

The derivative of \(f(x)\) with respect to \(x\), denoted \(f'(x)\), is the function defined as

\[f'(x) = \lim_{h\to 0} \frac{f(x+h) - f(x)}{h},\]

and the domain of \(f'(x)\) is the set of all \(x\) where the limit exists.

Notation

For a given function, \(y = f(x)\), each of the following symbols refers to the derivative of \(f(x)\) with respect to \(x\).

\[f'(x) \hspace{30pt} y' \hspace{30pt} \frac{d}{dx}f(x) \hspace{30pt} \frac {dy}{dx}\]

The Equation of a Tangent Line

The equation of the line tangent to \(f(x)\) at \(x=a\) is given by

\[y = f'(a)(x-a) + f(a)\]

The above equation is equivalent to the point-slope equation of a line (i.e., \(y=m(x-a) + b\)) where the slope, \(m\), is equal to \(f'(a)\), and the line goes through the point \((a,b)\), where \(b = f(a)\).

Computing Derivatives Using the Limit Definition

Simplify the Difference Quotient

When computing the derivative, \(f'(x)\), using its limit definition, it turns out that the limit will most likely be an indeterminate form of type \(0/0\). This means that to evaluate the limit, we’ll have to simplify the difference quotient

\[\frac{f(x+h) - f(x)}{h}\]

until we can cancel out the factor of \(h\) in the denominator. This simplification will usually consist of some combination of expanding (e.g., FOIL) and/or rationalization.

Once the factor of \(h\) in the denominator has been cancelled out, we can evaluate the limit by plugging in \(h=0\).

Example 1

Equation of a tangent line

Compute the slope of the line tangent to \(f(x)=3x^2+12\) at \(x=5\) using the limit definition of the derivative. Then write down the equation of the line tangent to \(f(x)\) at \(x=5\).

Step 1:   Write down the limit definition of a derivative.

\[ f'(x)=\lim_{h \to 0} \frac{f(x+h)-f(x)}{h}\]

Remember: \(f(x+h)\) means that we take \(f(x)\) and replace every occurrence of \(x\) with \((x+h)\). For example, if \(f(x) = x^2\), then \(f(x+h)=(x+h)^2=x^2+2xh+h^2.\)

Step 2:   Plug   \(f(5+h)\)   and   \(f(5)\)   into definition.

Recall that the slope of the line tagent to \(f(x)\) at \(x=5\) is given by \(f'(5)\). To compute \(f'(5)\), plug \(f(5+h) = 3(5+h)^2 + 12\) and \(f(5) = 3(5)^2 + 12 = 87\) into the limit definition of the derivative.

\[\begin{align*} f'(5) &=\lim_{h \to 0} \frac{f(5+h) - f(5)}{h} && \text{limit definition of $f'(5)$}\\ \\ &=\lim_{h \to 0} \frac{[3(5+h)^2+12]-[87]}{h} \end{align*}\]

Step 3:   Simplify the Difference Quotient

Simplify until we can factor out an \(h\) in the numerator and cancel it with the factor of \(h\) in the denominator.

\[\begin{align*} \frac{f(5+h) - f(5)}{h} &= \frac{[3(5+h)^2+12]-87}{h}\\ \\ &= \frac{[3(25+10h+h^2)+12]-87}{h} && \text{FOIL $(5+h)^2$}\\ \\ &= \frac{75+30h+3h^2+12-87}{h} && \text{distribute the 3}\\ \\ &= \frac{30h+3h^2}{h} && \text{simplify} \\ \\ &= \frac{h(30+3h)}{h} && \text{factor out $h$ in the numerator} \\ \\ &= 30+3h && \text{cancel the factor of $h$ in the numerator and denominator} \end{align*}\]

The last step of cancelling out the \(h\) assumes \(h\neq 0\). Note that when we evaluate the limit as \(h\) goes to zero in the next step, this will be a valid assumption.

Step 4:   Evaluate the limit.

\[\begin{align*} f'(5) &= \lim_{h \to 0} \frac{f(5+h) - f(5)}{h} \\ &= \lim_{h \to 0} 30+3h && \text{from Step 3} \\ &= 30+3(0) &&\text{plug in $h=0$}\\ &= 30 && \text{simplify} \end{align*}\]

Step 5:   Write down the equation of the tangent line.

From Steps 2 and 4, we know \(f(5) = 87\) and \(f'(5) = 30\). Therefore, the equation of the tangent line is given by

\[y = 30(x-5) + 87\]

Example 2

Compute the derivative at a point

Compute the derivative of \(f(x)=\dfrac{3}{x+2}\) at \(x=1\) using the limit definition of the derivative.

Step 1:   Write down the limit definition of a derivative.

\[ f'(x)=\lim_{h \to 0} \frac{f(x+h)-f(x)}{h}\]

Step 2:   Plug   \(f(1+h)\)   and   \(f(1)\)   into definition.

To compute \(f'(1)\), plug \(f(1+h) = \frac{3}{1+h+2} = \frac{3}{3+h}\) and \(f(1) = \frac{3}{1+2} = 1\) into the limit definition of the derivative.

\[\begin{align*} f'(1) &= \lim_{h \to 0} \frac{f(1+h) - f(1)}{h} && \text{limit definition of $f'(1)$}\\ \\ &= \lim_{h \to 0} \frac{\frac{3}{3+h}-1}{h} \end{align*}\]

Step 3:   Simplify the Difference Quotient

Simplify until we can cancel out the factor of \(h\) in the denominator.

\[\begin{align*} \frac{f(1+h) - f(1)}{h} &= \frac{\frac{3}{3+h}-1}{h} \\ \\ &= \left(\frac{3}{3+h}-1\right) \frac{1}{h} && \text{dividing by $h$ is the same as multiplying by $1/h$} \\ \\ &= \left(\frac{3}{3+h}-\frac{3+h}{3+h}\right) \frac{1}{h} && \text{get a common denominator} \\ \\ &= \left(\frac{3 - (3+h)}{3+h}\right) \frac{1}{h} && \text{subtract numerators}\\ \\ &= \left(\frac{3 - 3-h}{3+h}\right) \frac{1}{h} && \text{distribute the minus sign} \\ \\ &= \left(\frac{-h}{3+h}\right) \frac{1}{h} && \text{simplify the numerator}\\ \\ &= -\frac{1}{3+h} && \text{cancel the factor of $h$ in the numerator and denominator} \end{align*}\]

Step 4:   Evaluate the limit.

\[\begin{align*} f'(1) &= \lim_{h \to 0} \frac{f(1+h) - f(1)}{h} \\ &= \lim_{h \to 0} -\frac{1}{3+h} && \text{from Step 3} \\ &= -\frac{1}{3+0} &&\text{plug in $h=0$}\\ &= -\frac{1}{3} && \text{simplify} \end{align*}\]

Therefore, the derivative of \(f(x)\) at \(x=1\) is equal to \(-1/3\).

Example 3

Derivative of a square root function

Compute the derivative of \(f(x)=3\sqrt{x}\) using the limit definition of the derivative.

Step 1:   Write down the limit definition of a derivative.

\[ f'(x)=\lim_{h \to 0} \frac{f(x+h)-f(x)}{h} \]

Step 2:   Plug   \(f(x+h)\)   and   \(f(x)\)   into definition.

Plug \(f(x+h) = 3\sqrt{x+h}\) and \(f(x) = 3\sqrt{x}\) into the limit definition of the derivative.

\[\begin{align*} f'(x) = \lim_{h \to 0} \frac{3\sqrt{x+h}-3\sqrt{x}}{h} = \lim_{h \to 0} \frac{3(\sqrt{x+h}-\sqrt{x})}{h} \end{align*}\]

Step 3:   Rationalize, FOIL, and simplify.

\[\begin{align*} f'(x) &= \lim_{h \to 0} \frac{3(\sqrt{x+h}-\sqrt{x})}{h}\cdot \frac{\sqrt{x+h}+\sqrt{x}}{\sqrt{x+h}+\sqrt{x}} && \hbox{rationalize} \\ \\ &= \lim_{h \to 0} \frac{3(\sqrt{x+h}-\sqrt{x})(\sqrt{x+h}+\sqrt{x})}{h(\sqrt{x+h}+\sqrt{x})} \\ \\ &= \lim_{h \to 0} \frac{3(\sqrt{x+h}\sqrt{x+h} + \sqrt{x+h}\sqrt{x}-\sqrt{x}\sqrt{x+h} - \sqrt{x}\sqrt{x})}{h(\sqrt{x+h}+\sqrt{x})} && \hbox{FOIL} \\ \\ &= \lim_{h \to 0} \frac{3(\cancel{x}+h + \cancel{\sqrt{x+h}\sqrt{x}}-\cancel{\sqrt{x}\sqrt{x+h}} - \cancel{x})}{h(\sqrt{x+h}+\sqrt{x})} && \hbox{simplify} \\ \\ &= \lim_{h \to 0} \frac{3 h}{h(\sqrt{x+h}+\sqrt{x})} \end{align*}\]

Notice how making use of the formula \((\sqrt{A} - \sqrt{B})(\sqrt{A} + \sqrt{B}) = A - B\) can help eliminate some of the above computations.

Step 4:   Cancel the   \(h\)   in the numerator with the   \(h\)   in the denominator.

\[f'(x) = \lim_{h \to 0} \frac{3 \cancel{h}}{\cancel{h}(\sqrt{x+h}+\sqrt{x})} = \lim_{h \to 0} \frac{3}{\sqrt{x+h}+\sqrt{x}} \]

Step 5:   Evaluate the limit.

\[\begin{align*} f'(x) &= \lim_{h \to 0} \frac{3}{\sqrt{x+h}+\sqrt{x}} \\ &= \frac{3}{\sqrt{x + 0}+\sqrt{x}} && \text{plug in $h=0$}\\ &= \frac{3}{\sqrt{x}+\sqrt{x}} && \text{simplify}\\ &= \frac{3}{2\sqrt{x}} && \text{combine like terms} \end{align*}\]

Therefore, the derivative of \(f(x)\) is equal to \(\frac{3}{2\sqrt{x}}\).