Elasticity & Total Revenue

Relationship between Elasticity and Total Revenue

1. Total Revenue is increasing for those values of \(p\) where \(E(p) < 1\), that is, when demand is inelastic.

2. Total Revenue is decreasing for those values of \(p\) where \(E(p) > 1\), that is, when demand is elastic.

3. Total Revenue is maximized for those values of \(p\) where \(E(p) = 1\), that is, when demand is unitary.

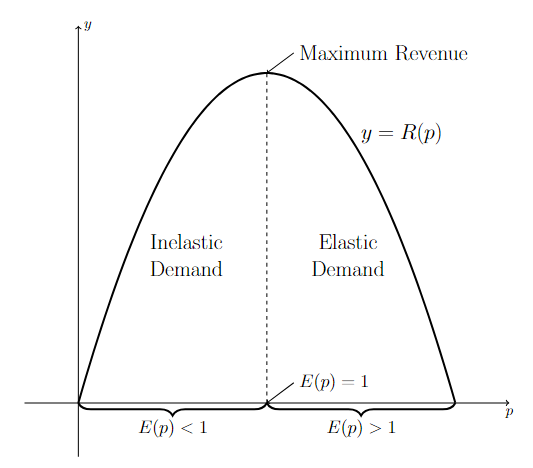
Long Text Description

There is a horizontal p-axis and a vertical y-axis. A concave down quadratic looking function R(p) is graphed on these axes. R(p) starts out at the origin increasing and concave down, comes to a maximum value at a point labeled “maximum revenue,” and is decreasing and concave down from there to a p-intercept. There is a vertical dotted line between a point on the p-axis labeled “E(p) = 1” and the “Maximum Revenue” point. The area to the left of this line is labeled “Inelastic Demand”. The area to the right of the line is labeled “Elastic Demand”. The line between the origin and “E(p) = 1” is labeled E(p) < 1 and the line between “E(p) = 1” and the p-intercept on the right is labeled “E(p) > 1.”

How a Change in Price Affects Total Revenue

1. Any price movement towards the unitary price increases total revenue.

2. Any price movement away from the unitary price decreases total revenue.

Example 1

Elasticity of demand

The demand equation for widgets is given by

\[ p = 2 - \frac{x}{10}. \]

Compute \(E(0.5)\) and \(E(1.5)\) and interpret the results.

Step 1:   Determine   \(x = f(p)\).

In other words, solve for demand \(x\), in terms of price \(p\), using the demand equation, if possible.

\[\begin{align*} p &= 2 - \frac{x}{10} && \hbox{demand equation}\\ 10p &= 20 - x && \hbox{multiply both sides by $10$}\\ x + 10p &= 20 && \hbox{add $x$ to both sides}\\ x &= 20 - 10p && \hbox{subtract $10p$ from both sides} \end{align*}\]

Therefore, \(f(p) = 20-10p\).

Step 2:   Compute   \(f'(p)\).

\[\begin{align*} f'(p) &= \frac{d}{dp}(20-10p) = -10 \end{align*}\]

Step 3:   Compute   \(E(p)\).

\[\begin{align*} E(p) = -\frac{pf'(p)}{f(p)} &= -\frac{p(-10)}{20-10p}\\ &= \frac{10p}{20-10p} \end{align*}\]

Step 4:   Calculate   \(E(0.5)\).

\[\begin{align*} E(0.5) &= \frac{10\cdot0.5}{20-10\cdot 0.5}\\ &= \frac{5}{20-5}\\ &= \frac{1}{3} \end{align*}\]

Since \(E(0.5) < 1\), demand is inelastic when the price is $0.50 and total revenue would increase if the price increases.

Step 5:   Calculate   \(E(1.5)\).

\[\begin{align*} E(1.5) &= \frac{10\cdot1.5}{20-10\cdot1.5}\\ &= \frac{15}{20-15}\\ &= 3 \end{align*}\]

Since \(E(1.5) > 1\), demand is elastic when the price is $1.50 and total revenue would increase if the price decreases.

Example 2

Unitary demand

Given the demand equation

\[x + \frac{p}{6} -50 = 0\]

where \(p\) represents the price in dollars and \(x\) the number of units, determine the value of \(p\) where demand is unitary and interpret the result.

Step 1:   Determine   \(x = f(p)\).

In other words, solve for demand \(x\), in terms of price \(p\), using the demand equation, if possible.

\[\begin{align*} x + \frac{p}{6} -50 &= 0 && \hbox{demand equation}\\ x + \frac{p}{6} &= 50 && \hbox{add $50$ to both sides}\\ x &= 50 - \frac{p}{6} && \hbox{subtract $p/6$ from both sides} \end{align*}\]

Therefore, \(f(p) = 50 - \dfrac{p}{6}\).

Step 2:   Compute   \(f'(p)\).

\[\begin{align*} f'(p) &= \frac{d}{dp}\left(50 - \frac{p}{6}\right)\\ &= \frac{d}{dp}\left(50 - \frac{1}{6}p\right)\\ &= -\frac{1}{6} \end{align*}\]

Step 3:   Compute   \(E(p)\).

\[\begin{align*} E(p) = -\frac{pf'(p)}{f(p)} &= -\frac{p(-1/6)}{50 - p/6}\\ &= \frac{p(1/6)}{50 - p/6}\\ &= \frac{p}{50 - p/6} \cdot \frac{1}{6} \\ &=\frac{p}{(50 - p/6)6}\\ &= \frac{p}{300 - p} \end{align*}\]

Step 4:   Recall that demand is unitary when   \(E(p) = 1\).

Therefore, set \(E(p) = 1\) and solve for \(p\).

\[\begin{align*} \frac{p}{300 - p} &= 1 && \hbox{set $E(p) = 1$}\\ p &= 300 - p && \hbox{multiply both sides by $300-p$}\\ 2p &= 300 && \hbox{add $p$ to both sides}\\ p &= 150 && \hbox{divide both sides by $2$} \end{align*}\]

Therefore, when the price is $150, demand is unitary and total revenue is maximized.

Example 3

Unitary demand

Given the demand equation

\[x^2 + 6p = 180\]

where \(p\) represents the price in dollars and \(x\) the number of units, determine the value of \(p\) where demand is unitary and interpret the result.

Step 1:   Determine   \(x = f(p)\).

In other words, solve for demand \(x\), in terms of price \(p\), using the demand equation, if possible.

\[\begin{align*} x^2 + 6p &= 180 && \hbox{demand equation}\\ x^2 &= 180-6p && \hbox{subtract $6p$ from both sides}\\ x&= \sqrt{180-6p} && \text{take the square root of both sides, $x\geq 0$} \end{align*}\]

Therefore, \(f(p) = \sqrt{180-6p}\).

Step 2:   Compute   \(f'(p)\).

\[\begin{align*} f'(p) &= \frac{d}{dp}\sqrt{180-6p}\\ &= \frac{d}{dp}(180-6p)^{1/2} && \text{}\\ &=\frac{1}{2}(180-6p)^{-\frac{1}{2}} (-6) && \text{using the generalized power rule}\\ &=\frac{-3}{\sqrt{180-6p}} && \text{simplify} \end{align*}\]

Step 3:   Compute   \(E(p)\).

\[\begin{align*} E(p) = -\frac{p f'(p)}{f(p)} &=-\frac {p(-3 / \sqrt{180-6p})}{\sqrt{180-6p}}\\ &= \frac {p}{\sqrt{180-6p}} \cdot \frac{3}{\sqrt{180-6p}}\\ &= \frac {3p}{(\sqrt{180-6p})(\sqrt{180-6p})}\\ &= \frac{3p}{180-6p} && \text{combine the square roots} \end{align*}\]

Step 4:   Recall that demand is unitary when   \(E(p) = 1\).

Therefore, set \(E(p) = 1\) and solve for \(p\).

\[\begin{align*} \frac{3p}{180-6p} &= 1 && \hbox{set $E(p) = 1$}\\ 3p &= 180-6p && \hbox{multiply both sides by $180-6p$}\\ 9p &= 180 && \hbox{add $6p$ to both sides}\\ p &=20 && \hbox{divide both sides by $9$} \end{align*}\]

Therefore, when the price is $20, demand is unitary and total revenue is maximized.