Try It Yourself#
Exercise 1#
Find the \(x\)-coordinates of the relative extrema of \(g(x) = 3x^2 + 5x +5\)
Show answer
Answer: rel. min. at \(x=-5/6\)
Exercise 2#
Find the \(x\)-coordinates of the relative extrema of \(f(x) = x^3 - 27x + 9\).
Show answer
Answer: rel. max. at \(x=-3\), rel. min. at \(x=3\)
Exercise 3#
Find the \(x\)-coordinates of the relative extrema of \(h(x) = x^2 + \dfrac{16}{x}\).
Show answer
Answer: rel. min. at \(x=2\)
Exercise 4#
Find the absolute extrema of \(g(x) = 2x^3 + 18x^2 + 48x + 17\) on the interval \([0,1]\).
Show answer
Answer: abs. min. value is \(17\), abs. max. value is \(85\)
Exercise 5#
Find the absolute extrema of \(g(x) = 42x^3 + 33x^2 - 36x + 12\) on the interval \([0,1]\).
Show answer
Answer: abs. min. value is \(141/27\), abs. max. value is \(51\)
Exercise 6#
Find the absolute extrema of \(f(x) = x + \dfrac{49}{x} + 9\) on the interval \([1,98]\).
Show answer
Answer: abs. min. value is \(23\), abs. max. value is \(215/2\)
Exercise 7#
Find the absolute extrema of \(f(x) = \dfrac{7x}{x^2+9}\) on the interval \([0,9]\).
Show answer
Answer: abs. min. value is \(0\), abs. max. value is \(7/6\)
Exercise 8#
A game box manufacturer determines that in order to sell \(x\) units, the price per unit in dollars must be \(p(x) = 250 - x\). The manufacture also determines that the total cost of producing \(x\) units is given by \(C(x) = 2500 + 10x\). How many units must the company produce and sell in order to maximize profit?
Show answer
Answer: \(120\) units
Exercise 9#
A printer needs to make a poster that will have a total area of \(200\) in\(^2\) and will have \(1\) inch margins on the sides, a \(2.5\) inch margin on the top, and a \(1.5\) inch margin on the bottom. Find the dimensions of the poster that maximize the area of the printed (i.e., shaded) area?
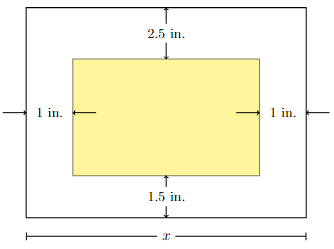
Long Text Description
There are two rectangles, one inside of the other. The smaller rectangle is colored in yellow, and the space inside the larger rectangle but outside the smaller is not colored. The length between the top of the yellow rectangle and the top of the larger one is labelled as 2.5 inches. The length between the left side of the yellow rectangle and the left side of the larger rectangle is labelled 1 inch. The length between the bottom of the yellow rectangle and the bottom of the larger rectangle is labelled as 1.5 inches.
Show answer
Answer: width is \(10\) in., height is \(20\) in.