Try It Yourself

Exercise 1

Let \(f(x) = \dfrac{x - 1}{2x - 6}\) and \(g(x) = \sqrt{2x + 1}\).

Determine the domain for \(f+g\), \(f-g\), \(fg\), and \(f/g\).

Show answer

Answer: Domain for \(f+g\), \(f-g\), \(fg\): \([-1/2,3) \cup (3,\infty)\); Domain for \(f/g\): \((-1/2,3) \cup (3,\infty)\)

Exercise 2

Let \(f(x) = 3\sqrt{x}\) and \(g(x) = \dfrac{x}{2x-1}\).

Determine the rule for the composite functions \(f \circ g\) and \(g \circ f\).

Show answer

Answer: \((f\circ g)(x) = 3\sqrt{x/(2x-1)}\); \((g\circ f)(x) = 3\sqrt{x}/(6\sqrt{x}-1)\)

Exercise 3

A manufacturer of Everlasting LED lightbulbs has fixed monthly costs of $25,000 and a processing cost of $3 for each lightbulb produced. Assuming each lightbulb sells for $5, compute the break-even point.

Show answer

Answer: 12,500 lightbulbs

Exercise 4

Determine the degree of the polynomial

\[(x^4 + x)^2(x^3 + x + 1)^5.\]

Show answer

Answer: \(23\)

Exercise 5

Write

\[\dfrac{x}{x^2-4} - \dfrac{2x+1}{x+5}\]

as a ratio of polynomials and determine its domain.

Show answer

Answer: \((-2x^3 + 13x + 4)/(x^3 + 5x^2 - 4x - 20)\), Domain: \((-\infty,-5) \cup (-5,-2) \cup (-2,2) \cup (2,\infty)\)

Exercise 6

The demand and supply functions for The Best of Math 110: A DVD Collection are:

\[\begin{align*} p = d(x) &= -x^2 - 2x + 100\\ p = s(x) &= 2x^2 + 4x - 140 \end{align*}\]

where \(x\) is the number of thousands of DVDs and \(p\) is in dollars. Determine the market equilibrium values.

Show answer

Answer: Equilibrium quantity = 8000; Equilibrium price = $20

Exercise 7

A rectangular field is to be enclosed by 200 feet of fence. One side of the field is a building, so fencing is not required on that side.

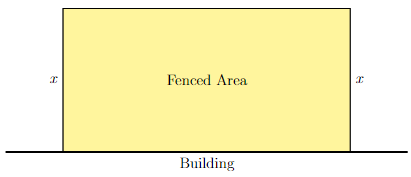
Long Text Description

There is a thick black line representing the side of a building. Above this is a yellow rectangle representing the area enclosed by a fence. The height of this rectangle is marked as x.

If \(x\) denotes the length of one side of the rectangle perpendicular to the building, determine the function in the variable \(x\) giving the area (in square feet) of the fenced-in region and state the appropriate domain.

Show answer

Answer: Area: \(200x - 2x^2\), Domain: \([0,100]\)

Exercise 8

A game box manufacturer determines that in order to sell \(x\) units, the price per unit in dollars must be \(p(x) = 250 - x\). The manufacture also determines that the total cost of producing \(x\) units is given by \(C(x) = 2500 + 10x\). Determine the profit as a function of \(x\) and state the appropriate domain.

Show answer

Answer: Profit: \(240x - x^2 - 2500\), Domain: \([0,250]\)

Exercise 9

A printer needs to make a poster that has a total area of \(200\) in\(^2\), \(1\) inch margins on the sides, a \(2.5\) inch margin on the top, and a \(1.5\) inch margin on the bottom. If \(x\) denotes the width (in inches) of the poster, find a function in the variable \(x\) giving the area of the printed (i.e., shaded) region and state the appropriate domain.

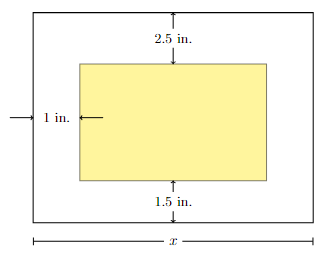
Long Text Description

There is a large white rectangle, representing the total area of a poster. There is a yellow rectangle inside the larger one, representing the area that may be printed on to give the required margins. The distance between the tops of the rectangles is marked as 2.5 inches. The distance between the corresponding sides of the two rectangles is given as 1 inch. The distance between the bottoms of both rectangles is given as 1.5 inches. The width of the white rectangle is given as x.

Show answer

Answer: Area: \((x-2)(200/x-4)\), Domain: \([2,50]\)