Inflection Points

Definition

Definition

An inflection point is a point on the graph of a continuous function where the concavity changes.

Example 1

Inflection point

An inflection point occurs at a point on a graph where the concavity changes from concave up to concave down or from concave down to concave up.

Long Text Description

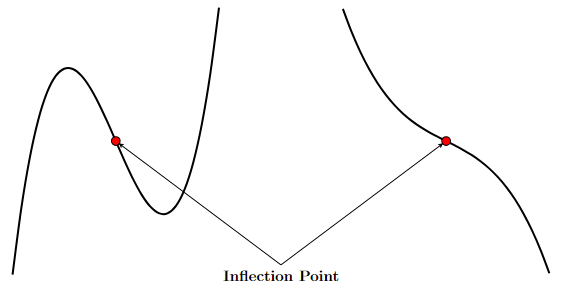
The graphs of two functions are presented without axes.

The left hand function is increasing and concave down, begins decreasing and being concave down at a rounded corner, passes through a red marked point, is decreasing and concave up, and is increasing and concave up after a rounded corner.

The right hand function is decreasing and concave up, passes through a red marked point, and then is decreasing and concave down.

There is a label reading “Inflection Points” with arrows from it pointing at both red marked points.

Finding Inflection Points using the Second Derivative

How to Find Inflection Points of a Function

1. Find all values of \(x\) such that \(f''(x) = 0\) or \(f''(x)\) does not exist.

2. Break up domain of \(f\) into open intervals between values found in Step 1.

3. Evaluate \(f''(x)\) at one value, \(c\), from each interval found in Step 2.

   • If \(f''(x)\) changes sign at \(x=c\) and \(x=c\) is in the domain of \(f\), then the point \((c,f(c))\) is an inflection point of \(f\).

Example 2

Find inflection points

Find the inflection points of \(f(x) = x^3 + 10x - \dfrac{3}{x}\).

Step 1:   Compute   \(f''(x)\).

\[\begin{align*} f'(x) &= \frac{d}{dx} (x^3 + 10x - 3x^{-1}) \\ &= 3x^2 + 10 + 3x^{-2} & \\ & \\ f''(x) &= \frac{d}{dx}(3x^2 + 10 + 3x^{-2}) \\ &= 6x - 6x^{-3} \\ &= 6x - \frac{6}{x^3} \\ &= \frac{6x^4}{x^3} - \frac{6}{x^3} && \hbox{get a common denominator}\\ &= \frac{6x^4 - 6}{x^3} \\ &= \frac{6(x^4 - 1)}{x^3} \\ &= \frac{6(x^2 - 1)(x^2+1)}{x^3} && \text{factor $x^4 - 1 = (x^2)^2 - 1^2$ as a difference of squares}\\ &= \frac{6(x - 1)(x+1)(x^2+1)}{x^3} && \hbox{factor $x^2 - 1$ as a difference of squares} \end{align*}\]

Step 2:   Find all values of   \(x\)   such that   \(f''(x) = 0\).

\(f''(x) = 0\) when \(x=1\) and \(x=-1\).

Step 3:   Find all values of   \(x\)   such that   \(f''(x)\)   does not exist.

\(f''(x)\) does not exist when \(x^3 = 0\) (i.e., when \(x=0\)).

Step 4:   Break up the domain of   \(f\).

Break up the domain of \(f\) at each value found in Steps 2 and 3. Plug one number from each subinterval into \(f''(x)\) to determine the sign of \(f''(x)\) on that interval.

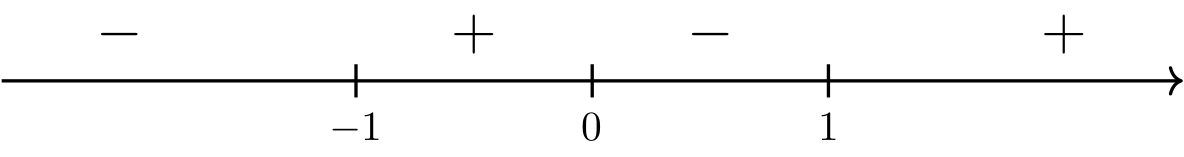
Fig. 8 Sign analysis of \(f''(x) = \frac{6(x - 1)(x+1)(x^2+1)}{x^3}\).

Long Text Description

A number line with positive and negative signs assigned to intervals, with negative to the left of negative one, positive between negative one and zero, negative between zero and one, and positive to the right of one.

Notice that \(f''(x)\) changes sign at \(x=-1\), \(x=0\), and \(x=1\), however, \(x=0\) is not in the domain of \(f\) and cannot correspond to an inflection point. Therefore, \((-1, -8)\) and \((1,8)\) are the only inflection points of \(f\).

Points of Diminishing & Increasing Returns

Definition

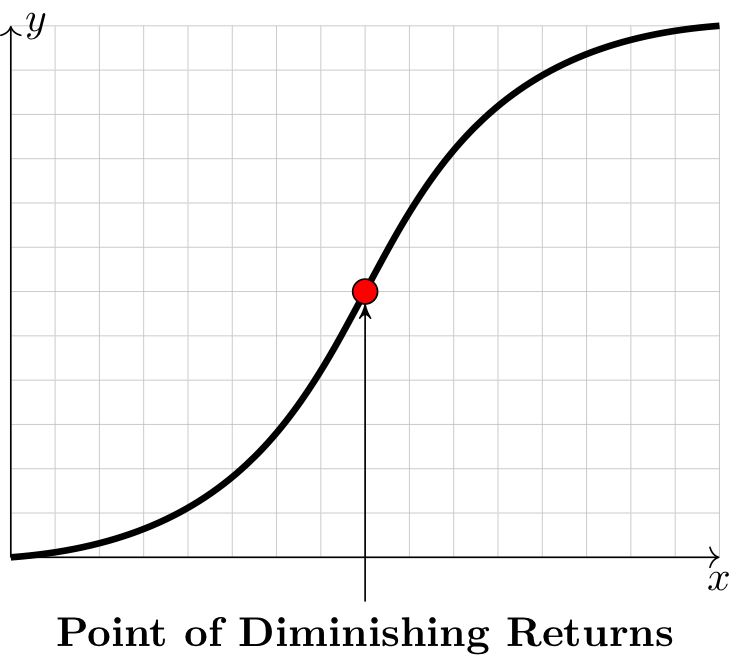
A point of diminishing returns is an inflection point appearing where a function is increasing and the concavity changes from concave up to concave down.

Long Text Description

There is a horizontal x-axis. There is a vertical y-axis. There is an increasing curve plotted on these axes. There is a point, colored red and labeled “Point of Diminishing Returns” along the curve. To the left of this point, the curve is concave up. To the right, this curve is concave down.

Definition

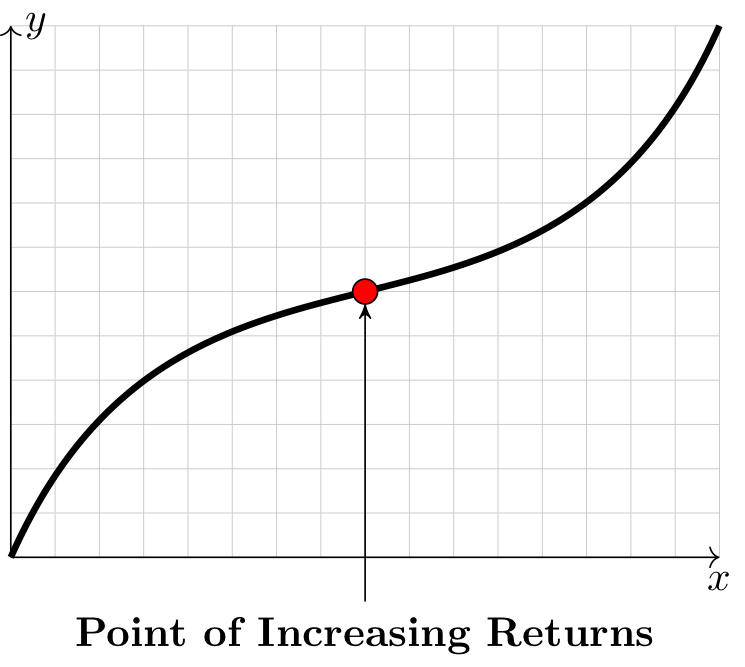
A point of increasing returns is an inflection point appearing where a function is increasing and the concavity changes from concave down to concave up.

Long Text Description

There is a horizontal x-axis. There is a vertical y-axis. There is an increasing curve plotted on these axes. There is a point, colored red and labeled “Point of Increasing Returns” along the curve. To the left of this point, the curve is concave down. To the right, this curve is concave up.

Example 3

Find point of diminishing or increasing returns

Determine whether or not \(f(x) = 3x^3-18x^2+81x+90\) has a point of diminishing or increasing return.

Step 1:   Compute   \(f'(x)\).

\[\begin{align*} f'(x) &= 9x^2 - 36x + 81 \\ &= 9(x^2 - 4x + 9) \end{align*}\]

Step 2:   Compute   \(f''(x)\).

\[\begin{align*} f''(x) &= 18x - 36 \\ &= 18(x-2) \end{align*}\]

Step 3:   Find and analyze inflection points.

Find inflection points, if any, and determine if each one corresponds to a point of diminishing return, increasing return, or neither.

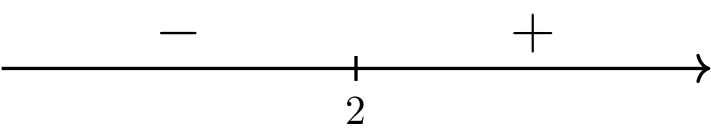
Fig. 9 Sign analysis of \(f''(x) = 18(x-2)\).

Long Text Description

A number line with positive and negative signs assigned to intervals, with negative to the left of two, and positive to the right of two.

Notice that \(f''(x) = 0\) only when \(x=2\). Furthermore, \(f'(2)\) is positive, which means that \(f(x)\) is increasing near \(x=2\). And lastly, since \(f''(x)\) changes sign from negative to positive at \(x=2\), \(f(x)\) has a point of increasing returns at \(x=2\).

Make Sure to Check that Function is Increasing

If the function \(f\) has an inflection point at \((c,f(c))\), but \(f'(c) < 0\) (i.e., the function is decreasing near the inflection point), then by definition, the function does not have a point of diminishing or increasing returns at \((c,f(c))\).