Functions, Domain, and Range#
Definitions#
Definition
A function is a rule that assigns to each element in a set \(A\) one and only one element in a set \(B\).
It is customary to denote a function by a letter of the alphabet, such as \(f\), \(g\), \(h\), etc.
Definition
The set \(A\) is called the domain of the function. The element in \(B\) that \(f\) associates with \(x\) is written as
(read “\(f\) of \(x\)”) and is called the value of \(f\) at \(x\).
Definition
The set of all possible values of \(f(x)\) resulting from all the possible values of \(x\) in its domain, is called the range of \(f(x)\).
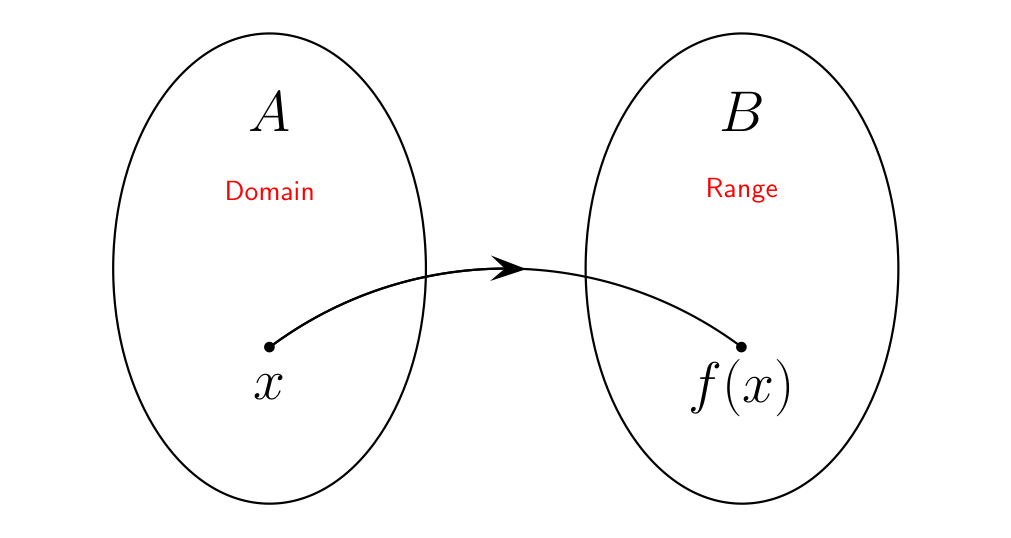
Fig. 1 Illustration of the domain and the range of a function#
Long Text Description
A diagram with two ovals, one on the left marked with A, labeled domain, and one on the right marked B and labeled range. There is an arrowed line representing the function f beginning at a point labeled x in the left oval, and ending in a point labeled f(x) in the right oval.
Definition
Suppose we are given the function \(y=f(x)\).
The variable \(x\) is called the independent variable.
The variable \(y\), whose value depends on \(x\), is called the dependent variable.
Domain Considerations#
Restrictions on the Domain
To determine the domain of a function, we need to find what restrictions, if any, are to be placed on the independent variable.
In many practical problems, the domain of a function is dictated by the context of the problem and any restrictions on the function itself. In this course, these restrictions will be limited to one or more of the following:
cannot take the square root of a negative number
cannot divide by zero
cannot take the logarithm of zero or a negative number
Example 1#
Find the domain and range
Determine the domain and range of \(f(x) = x^2 - 1\).
Step 1: Determine the domain of \(f\).
Since \(f\) does not include any division, square roots, or logarithms, its domain consists of all real numbers, \((-\infty,\infty)\).
Step 2: Determine the range of \(f\).
Since \(x^2 \geq 0\) for all real \(x\), by subtracting \(1\) from both sides of the inequality, we obtain \(f(x) = x^2 - 1 \geq -1\) for all real \(x\). Therefore, the range of \(f\) is \([-1,\infty)\).
Another way to determine the domain and range of \(f\) is to consider the graph of \(y = f(x)\). For this example, the graph of \(y = x^2 - 1\) is a parabola that opens up and is shifted down one unit, as illustrated below.
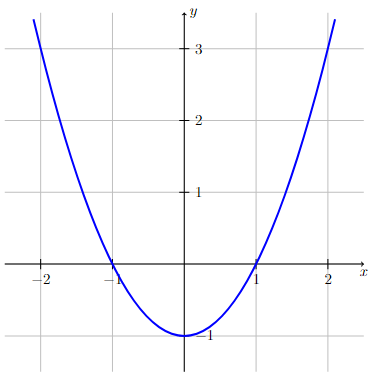
Long Text Description
There is a horizontal x-axis with the points -2, -1, 1, and 2 marked. There is a vertical y-axis with the points -1, 1, 2, and 3 marked. The graph of the concave up quadratic function y = x^2 - 1 is plotted. It has x-intercepts at the points (-1,0) and (1,0), and a rounded vertex at (0,-1).
The domain of \(f\) consists of all the different \(x\)-coordinates of points on the graph of \(f\), which is \((-\infty,\infty)\).
The range of \(f\) consists of all the different \(y\)-coordinates of points on the graph of \(f\), which is \([-1,\infty)\).
Example 2#
Find the domain
Determine the domain of \(g(x) = \dfrac{1}{\sqrt{x}}\).
Step 1: Consider how the square root restricts the domain.
Since \(g\) includes the square root function, \(\sqrt{x}\), we must assume that \(x\geq 0\).
Step 2: Consider how division restricts the domain.
Since \(g\) includes division, we must exclude any value of \(x\) that makes the denominator equal to zero. In this example, the denominator equals zero only when \(x=0\).
Step 3: Determine the domain of \(g\).
Based on the previous two steps, the domain of \(g\) consists of all real numbers greater than zero, which can be written in interval notation as \((0,\infty)\).
Domain Analysis#
The Sum, Difference, Product, and Quotient of Two Functions and their Domains
Let \(f\) and \(g\) be functions with domains \(A\) and \(B\), respectively. The sum, difference, product, and quotient of \(f\) and \(g\) are functions defined by
The domain of \(f+g\), \(f-g\), and \(fg\) consists of all values of \(x\) that appear in both \(A\) and \(B\), which is called the intersection of \(A\) and \(B\), and is denoted by \(A\cap B\).
The domain of \(f/g\) consists of \(A\cap B\) excluding all values of \(x\) such that \(g(x)=0\).
Example 3#
Find the domain
Let \(f(x) = \sqrt{x + 2}\) and \(g(x) = \sqrt{5-x}\). Determine the domain of \(f+g\), \(f-g\), \(fg\), and \(f/g\). Use interval notation to express each domain.
Step 1: Determine the domain of \(f\) and \(g\) separately.
The domain of \(f\) consists of all \(x\) such that \(x+2 \geq 0\), or equivalently, \(x \geq -2\). Therefore, the domain of \(f\) is \([-2,\infty)\).
The domain of \(g\) consists of all \(x\) such that \(5-x \geq 0\), or equivalently, \(x \leq 5\). Therefore, the domain of \(g\) is \((-\infty,5]\).
Step 2: Determine the domain of \(f+g\), \(f-g\), and \(fg\).
The domain of \(f+g\), \(f-g\), and \(fg\) is the intersection of \([-2,\infty)\) (i.e., \(-2 \leq x\)) and \((-\infty,5]\) (i.e., \(x \leq 5\)). In other words, the domain of all three functions consists of values of \(x\) such that \(-2 \leq x \leq 5\), or equivalently, \([-2,5]\).
Step 3: Determine the values of \(x\) such that \(g(x) = 0\).
Set \(g(x) = 0\).
Solve for \(x\) by squaring both sides.
And finally, adding \(5\) to both sides yields \(x=5\) (i.e., \(g(x) = 0\) only when \(x=5\)).
Step 4: Determine the domain of \(f/g\).
The domain of \(f/g\) consists of \([-2,5]\), excluding all values of \(x\) such that \(g(x) = 0\). In the previous step, we determined that the only value of \(x\) that satisfies \(g(x) = 0\) is \(x=5\), which must now be excluded from the domain. Therefore, the domain of \(f/g\) is \([-2,5)\).