Applications

Optimization Problems

Solving Optimization Problems

1. Assign a letter to each variable described in the problem. If appropriate, draw and label a figure.

2. Translate the problem description into an expression that includes the quantity to be optimized.

3. Use the conditions given in the problem to write the quantity to be optimized as a function of one variable. Note any restrictions to be placed on the domain of the function from the physical considerations of the problem.

4. Identify the critical points of the function, and determine the corresponding optimization values of the function over its domain using any of the optimization strategies discussed in class (e.g. First Derivative Test, Second Derivative Test, Graphing).

Example 1

Maximize profits

An apartment complex has 100 two-bedroom units. The monthly profit in dollars realized from renting out the apartments is given by:

\[P(x)=-20x^2+1720x-20,000\]

How many units must be rented to maximize profits?

Step 1: Draw a figure, if necessary.

A figure is not required to determine the numbers of units to rent to maximize the profit.

Step 2: Translate the problem description into an expression that includes the quantity to be optimized.

The expression to be optimized is given:

\[P(x)=-20x^2+1720x-20,000\]

Step 3: Use the given conditions/any physical constraints to write the quantity to be optimized as a function of one variable.

The expression to be optimized is given:

\[P(x)=-20x^2+1720x-20,000\]

and is already a function of a single variable \(x\). Observe that \(P(x)\) is continuous over the closed interval domain \([0,100]\).

Step 4: Find the critical points of \(P(x)\) on \((0,100)\), if any.

The expression to be optimized is:

\[P(x)=-20x^2+1720x-20,000\]

Computing \(P'(x)\):

\[\begin{align*} P'(x) &= -40x+1720 \end{align*}\]

\(P'(x) = 0\) when \(x = 1720/40 = 43\), which is in the open interval \((0,100)\). Therefore, \(x = 43\) is a critical point.

Since \(P(x)\) is continuous on the closed interval \([0,100]\), we could evaluate \(P(x)\) at \(x = 0\), \(x=43\), and \(x=100\) to determine the number of units that maximizes the profit.

Instead, observe that \(P(x)\) is a parabola that opens downward (i.e., \(P''(x) = -40\) which means that \(P(x)\) is concave down). This implies that the critical point at \(x=43\) must correspond to the maximum profit.

Therefore, profit is maximized when 43 units are rented out.

Example 2

Maximize area

A rectangular field is to be enclosed by a fence. One side of the fenced-in area is a building, so fencing is not required on that side. If we have 200 feet of fencing material, determine the dimensions of the largest field that can be enclosed by the fencing material.

Step 1: Draw a figure, if necessary.

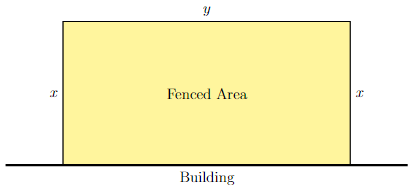
Long Text Description

There is a thick black horizontal line representing the edge of the building. Above that there is a grey rectangle representing the fenced area. The side lengths of the rectangle are height = x and width = y.

Step 2: Translate the problem description into an expression that includes the quantity to be optimized.

\[\text{Maximize: Area} = x \cdot y\]

Step 3: Use the given conditions/any physical constraints to write the quantity to be optimized as a function of one variable.

Since we have 200 feet of fencing material, the variables \(x\) and \(y\) must satisfy the following equation.

\[2x + y = 200\]

Solving for \(y\) yields \(y = 200 - 2x\). Substituting this into our formula for area from Step 2, we obtain \(A(x)\), the area of the region enclosed by the fence as a function of \(x\).

\[\begin{align*} A(x) &= x \cdot (200 - 2x) \\ &= 200x - 2x^2 \end{align*}\]

Note the following domain restriction: \(0 < x < 100\) since

\[x > 0 ~~~~ \hbox{ and } ~~~~ y = 200-2x > 0.\]

Step 4: Identify the critical points of the function, and determine the corresponding optimization values of the function over its domain.

Start by computing \(A'(x)\),

\[A'(x) = 200-4x\]

which equals zero when \(x = 200/4 = 50\).

We can check that \(x = 50\) corresponds to the maximum area by verifying that the second derivative is negative. Since \(A''(x) = -4 < 0\) for all \(x\) in the domain, and \(x=50\) is in the domain of \(A(x)\), we see that \(A(50)\) is the absolute maximum value of \(A(x)\) on \((0,100)\).

Solve for \(y\) to find the other dimension of the field:

\[\begin{align*} y &= 200 - 2x \\ &=2 00 - 2(50) \\ &= 100 \end{align*}\]

We conclude that the field with maximum area enclosed by 200 feet of fencing material is 50 feet deep and 100 feet wide.

Example 3

Minimize costs

A rectangular box with a square base and a volume of \(24\) ft\(^3\) has costs to construct of \(\$10 / \text{ft}^2\) for the sides, \(\$20 / \text{ft}^2\) for the top, and \(\$40 / \text{ft}^2\) for the base. Determine the dimensions of the box which minimize the total cost to construct the box.

Step 1: Draw a figure, if necessary.

Long Text Description

A two dimensional projective diagram of a three dimensional square prism, with the square face horizontal and of side length x, and height y.

Step 2: Translate the problem description into an expression that includes the quantity to be optimized.

\[\begin{align*} \text{Minimize: Cost} &= 40\cdot\text{(area of base)} + 10\cdot\text{(area of sides)} + 20\cdot\text{(area of top)} \\ &= 40x^2 + 10\cdot4xy + 20\cdot x^2 \\ &= 60x^2 + 40xy \end{align*}\]

Step 3: Use the given conditions/any physical constraints to write the quantity to be optimized as a function of one variable.

Since the volume of the box is given to be \(24\) ft\(^3\), the variables \(x\) and \(y\) must satisfy the following equation.

\[x^2y = 24\]

Solving for \(y\) yields \(y = 24/x^2\). Substituting this into our formula for cost in Step 2, we obtain \(C(x)\), the cost of constructing the box as a function of \(x\).

\[\begin{align*} C(x) &= 60x^2 + 40x\left(\frac{24}{x^2}\right) \\ &= 60x^2 + \frac{960}{x} \\ &= 60x^2 + 960x^{-1} \end{align*}\]

Note the following domain restriction: \(x > 0\) since each dimension of the box must be positive.

Step 4: Identify the critical points of the function, and determine the corresponding optimization values of the function over its domain.

Start by computing \(C'(x)\),

\[\begin{align*} C'(x) &= \frac{d}{dx}(60x^2 + 960x^{-1}) \\ \\ &= 60 \cdot 2x + 960(-1)x^{-2} \\ \\ &= 120x - 960x^{-2} \\ \\ &= 120x - \frac{960}{x^2}\\ \\ &= \frac{120x^3}{x^2} - \frac{960}{x^2} && \hbox{Get a common denominator}\\ \\ &= \frac{120x^3 - 960}{x^2} && \hbox{Combine numerators}\\ \\ &= \frac{120(x^3 - 8)}{x^2} && \hbox{Simplify numerator} \end{align*}\]

which equals zero when \(x^3 - 8 = 0\) (i.e., \(x = 2\)).

Finally, we can check that the critical point \(x = 2\) corresponds to the minimum cost by verifying that the second derivative is positive. Since

\[C''(x) = 120 + 1920x^{-3}\]

is positive for all \(x\) in the domain (i.e., \(x>0\)), and \(x=2\) is in the domain of \(C(x)\), we see that \(C(2)\) is the absolute minimum value of \(C(x)\) on \((0,\infty)\).

We can now solve for \(y\), and write down the dimensions of the box.

\[ y = \frac{24}{2^2}= 6\]

Therefore, the dimensions of the box that minimize the cost of construction are \(2 \times 2 \times 6\).

Example 4

Maximize profits

A computer manufacturer determines that in order to sell \(x\) units of a new computer, the price per unit in dollars must be:

\[p(x) = 2500 - 2x\]

The manufacturer also determines that the total cost of producing \(x\) units is given by:

\[C(x) = 3400 + 60x\]

Assuming all units produced can be sold, how many units must the company produce to maximize profit \(P(x)\)?

Step 1: Draw a figure, if necessary.

A figure is not required to determine the numbers of units required to maximize the profit.

Step 2: Translate the problem description into an expression that includes the quantity to be optimized.

The total profit function \(P(x)\) is given by:

\[\begin{align*} P(x) &=& R(x) - C(x) \\ &= x \cdot p(x) - C(x) \\ &= x \cdot (2500 - 2x) - (3400+60x) \\ &= 2500x-2x^2 - 3400 - 60x \\ &= -2x^2 + 2440x - 3400 \end{align*}\]

Step 3: Use the given conditions/any physical constraints to write the quantity to be optimized as a function of one variable.

The total profit function \(P(x)\) is given by:

\[P(x)=-2x^2+2440x-3400\]

Note the following domain restriction: \(0 < x < 1250\) since

\[x > 0 ~~~~ \hbox{ and } ~~~~ p(x)=2500-2x > 0.\]

Step 4: Identify the critical points of the function, and determine the corresponding optimization values of the function over its domain.

Start by computing \(P'(x)\):

\[P'(x) = -4x + 2440\]

which is equal to zero when \(x = 2440/4 = 610\). Note that \(x=610\) is in the domain of \(P(x)\).

We can confirm that \(x = 610\) corresponds to the maximum profit by verifying that the second derivative is negative. Since \(P''(x) = -4 < 0\) for all \(x\) in the domain, and \(x=610\) is in the domain, we see that \(P(610)\) is the absolute maximum profit.

Therefore, in order to maximize profits, the company must produce and sell 610 units (at a price of \(p(610) = 2500 - 2\cdot 610 = 1280\) dollars per unit).