Composition of Functions

Definitions

Definition

Let \(f\) and \(g\) be functions. The composition of \(f\) and \(g\) is the function \(f\circ g\) (read “\(f\) circle \(g\)” or “\(f\) composed with \(g\)”) defined by

\[(f\circ g)(x) = f(g(x))\]

The domain of \(f\circ g\) is the set of all \(x\) in the domain of \(g\) such that \(g(x)\) lies in the domain of \(f\), as illustrated below.

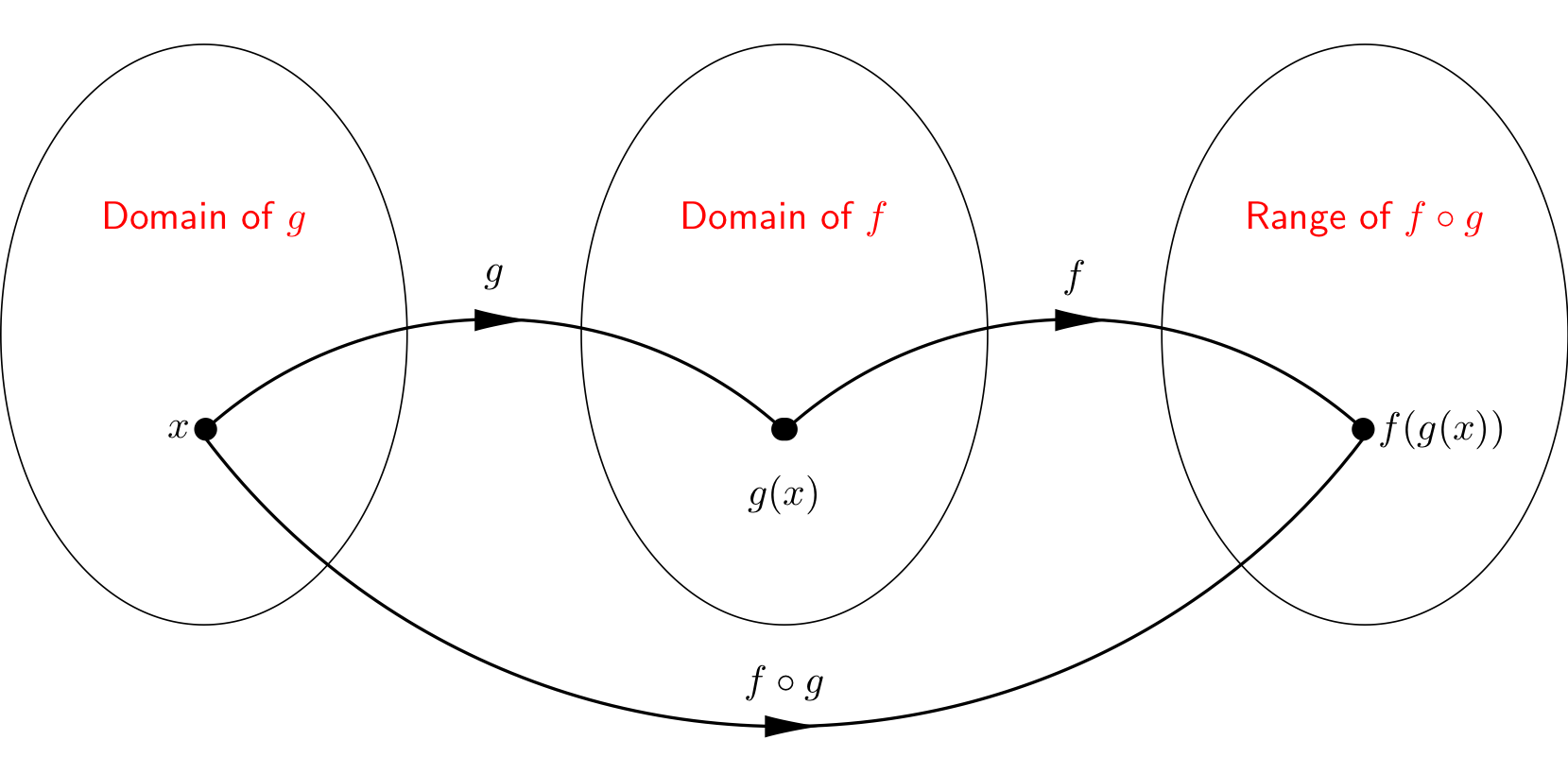
Fig. 2 Domain and range of a composition of functions

Long Text Description

A diagram with three ovals arranged from left to right. The leftmost oval is marked domain of g, the oval in the center is marked domain of f, and the right most oval is marked range of f composed with g. There is an arrowed line representing the function g beginning in the leftmost oval at a point labeled x and ending in the center oval at a point labeled g(x). There is a second arrowed line representing the function f beginning in the center oval at the point labeled g(x) and ending in the rightmost oval at a point labeled f(g(x)). There is a third arrowed line representing the function f composed with g beginning in the leftmost oval at the point labeled x and ends in the rightmost oval at the point labeled f(g(x)).

Important

The order of composition is significant. In other words, \(f\circ g\) and \(g\circ f\) are not necessarily the same functions.

Example 1

The composition of functions

Let

\[f(x) = \sqrt{7-x} \quad \text{ and } \quad g(x) = 3x + 2.\]

Determine if \(x=1\) and \(x=2\) are in the domain of \(f\circ g\) and if so, evaluate the function at the given value of \(x\).

Step 1:   Determine the domain of   \(f\)   and   \(g\).

The domain of \(f\) consists of all values of \(x\) such that \(7-x\geq 0\), or equivalently, \(x\leq 7\). The domain of \(g\) consists of all real numbers.

Step 2:   Determine if   \(x=1\)   is in the domain of   \(f \circ g\).

Note that \(x=1\) is in the domain of \(g\) and \(g(1) = 5\), which is in the domain of \(f\). Therefore \(x=1\) is in the domain of \(f\circ g\) and

\[\begin{align*} (f \circ g)(1) &= f(g(1)) \\ &= f(5) \\ &= \sqrt{2} \end{align*}\]

Step 3:   Determine if   \(x=2\)   is in the domain of   \(f \circ g\).

Note that \(x=2\) is in the domain of \(g\), but \(g(2) = 8\) is not in the domain of \(f\). Therefore \(x=2\) is not in the domain of \(f \circ g\).

Example 2

The composition of functions

Let

\[f(x) = \sqrt{7-x} \quad \text{ and } \quad g(x) = 3x + 2.\]

Determine the rule for the composite functions \(f \circ g\) and \(g \circ f\).

Step 1:   Determine the rule for the composite function   \(f \circ g\).

\[\begin{align*} (f \circ g)(x) &= f(g(x)) \\ &= f(3x+2) \\ &= \sqrt{7-(3x+2)} \\ &= \sqrt{7-3x-2} \\ &= \sqrt{5-3x} \end{align*}\]

The domain of \(f\circ g\) consists of all values \(x\) in the domain of \(g\) such that \(3x+2\) is in the domain of \(f\). As the above calculations show, this ultimately means that \(x\) must satisfy the inequality \(5-3x \geq 0\). Solving for \(x\) in this inequality yields

\[x \leq 5/3\]

and therefore, the domain of \(f\circ g\) is \((-\infty,5/3]\).

Step 2:   Determine the rule for the composite function   \(g \circ f\).

\[\begin{align*} (g \circ f)(x) &= g(f(x)) \\ &= g(\sqrt{7-x}) \\ &= 3\sqrt{7-x} + 2 \end{align*}\]

The domain of \(g\circ f\) consists of all values \(x\) in the domain of \(f\) such that \(\sqrt{7-x}\) is in the domain of \(g\). As the above calculations show, this ultimately means that \(x\) must satisfy the inequality \(7-x\geq 0\). Solving for \(x\) in this inequality yields

\[x \leq 7\]

and therefore, the domain of \(g\circ f\) is \((-\infty,7]\).