The First Derivative Test

Using the First Derivative to Classify Critical Points

The First Derivative Test

Suppose \(c\) is a critical point of the continuous function \(f\).

1. If \(f'(x)\) changes sign from positive to negative at \(x=c\), then \(f(c)\) is a relative maximum.

2. If \(f'(x)\) changes sign from negative to positive at \(x=c\), then \(f(c)\) is a relative minimum.

3. If \(f'(x)\) does not change sign at \(x=c\), then \(f(c)\) is not a relative extrema.

Example 1

Classify critical points based on graph of \(f'\)

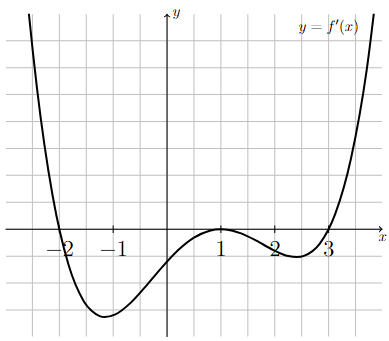
The following graph corresponds to \(f'(x)\), the first derivative of \(f(x)\).

Using the graph of \(f'(x)\), find and classify all critical points of \(f(x)\). You may assume that \(f'(x)\) is continuous for all \(x\) and \(f'(x) = 0\) only when \(x=-2\), \(x=1\), and \(x=3\).

Long Text Description

The graph of the derivative of a continuous function on the interval (-3,4). The derivative is equal to zero at x = -2, x = 1, and x = 3. The derivative decreases on the interval (-3,-1.2), increases on the interval (-1.2,1), decreases on the interval (1,2.4), and increases on the interval (2.4,4).

Step 1:   Determine the critical points of \(f(x)\).

Since \(f'(x)\) is continuous for all \(x\), and therefore defined for all \(x\), the only critical points of \(f(x)\) occur where \(f'(x) = 0\). And we were specifically told that the derivative is equal to zero only when \(x=-2\), \(x=1\), and \(x=3\), so these are the three critical points of \(f(x)\).

Step 2:   Classify each critical point.

Since \(f'(x)\) changes from positive to negative at \(x=-2\), \(f(x)\) has a relative maximum at \(x=-2\).

Since \(f'(x)\) does not change sign at \(x=1\), \(f(x)\) does not have a relative extrema at \(x=1\).

Since \(f'(x)\) changes from negative to positive at \(x=3\), \(f(x)\) has a relative minimum at \(x=3\).

Example 2

Classifying critical points using the first derivative test

In Example 1 of the previous section, we found that the critical points of

\[f(x) = \sqrt[3]{x^2-1}\]

were \(x=-1\), \(x=0\), and \(x=1\). Classify each critical point using the First Derivative Test.

Step 1:   Break up the domain of   \(f'(x)\)   at each critical point.

Plug in one number from each subinterval into \(f'(x)\) to determine the sign of \(f'(x)\) on each interval.

We have \(f'(x) = \dfrac{2x}{3(x^2 - 1)^{2/3}}\).

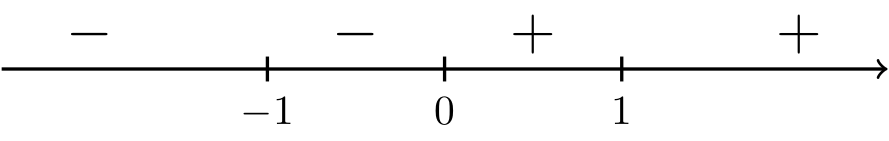
Fig. 4 Interval analysis of \(f'(x) = \dfrac{2x}{3(x^2 - 1)^{2/3}}\)

Long Text Description

A number line with positive and negative signs assigned to intervals, which are negative to the left of negative one, negative between negative one and zero, positive between zero and one, and positive to the right of one.

Step 2:   Classify each critical point.

Since \(f'(x)\) changes from negative to positive at \(x=0\), \(f(x)\) has a relative minimum at \(x=0\).

Since \(f'(x)\) does not change sign at \(x=-1\) and at \(x=1\), \(f(x)\) does not have relative extrema at these values of \(x\).

Example 3

Classifying critical points using the first derivative test

In Example 2 of the previous section, we found that the critical points of

\[f(x) = x^3 +3x^2 - 24x + 1\]

were \(x=-4\) and \(x=2\). Classify the critical point using the First Derivative Test.

Step 1:   Break up the domain of   \(f'(x)\)   at each critical point.

Plug in one number from each subinterval into \(f'(x)\) to determine the sign of \(f'(x)\) on each interval.

We have \(f'(x) = 3(x+4)(x-2)\).

Fig. 5 Interval analysis of \(f'(x) = 3(x+4)(x-2)\).

Long Text Description

A number line with positive and negative signs assigned to intervals, with positive to the left of negative four, negative between negative four and two, and positive to the right of two.

Step 2:   Classify each critical point.

Since \(f'(x)\) changes from positive to negative at \(x=-4\), \(f(x)\) has a relative maximum at \(x=-4\).

Since \(f'(x)\) changes from negative to positive at \(x=2\), \(f(x)\) has a relative minimum at \(x=2\).