The First Derivative Test

Using the First Derivative to Classify Critical Points

The First Derivative Test

Suppose \(c\) is a critical point of the continuous function \(f\).

1. If \(f'(x)\) changes sign from positive to negative at \(x=c\), then \(f(c)\) is a relative maximum.

2. If \(f'(x)\) changes sign from negative to positive at \(x=c\), then \(f(c)\) is a relative minimum.

3. If \(f'(x)\) does not change sign at \(x=c\), then \(f(c)\) is not a relative extrema.

Example 1

Classifying critical points using the first derivative test

In Example 1 from Critical Points, we found that the critical points of

\[f(x)=2x^3-15x^2+36x+20\]

were \(x=2\) and \(x=3\). Classify each critical point using the First Derivative Test.

Step 1: Break up the domain of \(f'(x)\) at each critical point.

Plug in one number from each subinterval into \(f'(x)\) to determine the sign of \(f'(x)\) on each interval.

We have \(f'(x) = 6(x-2)(x-3)\).

Fig. 10 Interval analysis of \(f'(x) = 6(x-2)(x-3)\)

Long Text Description

A number line with positive and negative signs assigned to intervals, with positive to the left of two, negative between two and three, and positive to the right of three.

Step 2: Classify each critical point.

Since \(f'(x)\) changes from positive to negative at \(x=2\), \(f(x)\) has a relative maximum at \(x=2\).

Since \(f'(x)\) changes from negative to positive at \(x=3\), \(f(x)\) has a relative minimum at \(x=3\).

Example 2

Classifying critical points using the first derivative test

In Example 2 from Critical Points, we found that the only critical point of

\[f(x)=\frac{1}{x^2-1}\]

was \(x=0\). Classify the critical point using the First Derivative Test.

Step 1: Break up the domain of \(f'(x)\) at each critical point.

Plug in one number from each subinterval into \(f'(x)\) to determine the sign of \(f'(x)\) on each interval.

We have \(f'(x) = -\dfrac{2x}{(x^2-1)^2}\).

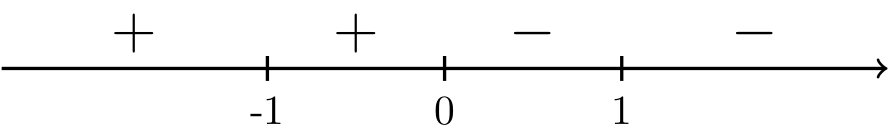
Fig. 11 Interval analysis of \(f'(x) = -\dfrac{2x}{(x^2-1)^2}\).

Long Text Description

A number line with positive and negative signs assigned to intervals, with positive to the left of negative one, positive between negative one and zero, negative between zero and one, and positive to the right of one.

Step 2: Classify each critical point.

Since \(f'(x)\) changes from positive to negative at \(x=0\), \(f(x)\) has a relative maximum at \(x=0\).