Exponential and Logarithmic Functions#
Definition and Properties of Exponential Functions#
Definition of an Exponential Function
For any constant \(b>0\) and \(b\neq 1\), the function
is called the exponential function with base \(b\).
Properties of Exponential Functions
For a function \(y = b^x\), the following properties hold:
Its domain is \((-\infty,\infty)\) and range is \((0,\infty)\).
Its graph passes through the point \((0,1)\) (i.e., \(b^0 = 1\)).
It is continuous on \((-\infty,\infty)\).
If \(b>1\)
\(b^x\) is increasing on \((-\infty,\infty)\)
\(\lim\limits_{x\to -\infty} b^x = 0\) and \(\lim\limits_{x\to \infty} b^x = \infty\)
If \(0 < b <1\)
\(b^x\) is decreasing on \((-\infty,\infty)\)
\(\lim\limits_{x\to -\infty} b^x = \infty\) and \(\lim\limits_{x\to \infty} b^x = 0\)
Example 1#
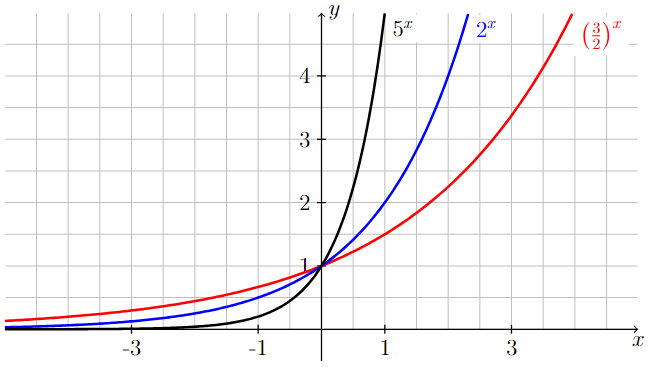
Graphs of exponential growth functions
The graphs of the exponential functions \(5^x\), \(2^x\), and \((3/2)^x\) are all shown below. Since the base associated with each function is greater than one, each exponential function is increasing and goes to infinity as \(x\) goes to infinity. For this reason, exponential functions with a base greater than one are referred to as exponential growth functions.
Long Text Description
The graphs of 5 to the power of x, 2 to the power of x, and 3/2 to the power of x are all shown on the same coordinate axes. The values -3, -1, 1, and 3 are marked on the x-axis and the values 1, 2, 3, and 4 are marked on the y-axis.
From left-to-right, the graph of y = 5 to the power of x starts very close to and above the x-axis. The graph slowly increases to the point (0,1) and continues to increase for positive values of x. The steepness of the curve also increases from left-to-right.
From left-to-right, the graph of y = 2 to the power of x starts very close to and above the graph of y = 5 to the power of x. The graph slowly increases to the point (0,1), at which point it crosses the graph of y = 5 to the power of x. It continues to increase for positive values of x, staying below the graph of y = 5 to the power of x. The steepness of the curve also increases from left-to-right, but it is not as steep as the graph of y = 5 to the power of x.
From left-to-right, the graph of y = 3/2 to the power of x starts very close to and above the graph of y = 2 to the power of x. The graph slowly increases to the point (0,1), at which point it crosses the graphs of y = 5 to the power of x and y = 2 to the power of x. It continues to increase for positive values of x, staying below the graph of y = 2 to the power of x. The steepness of the curve also increases from left-to-right, but it is not as steep as the graph of y = 2 to the power of x.
Example 2#
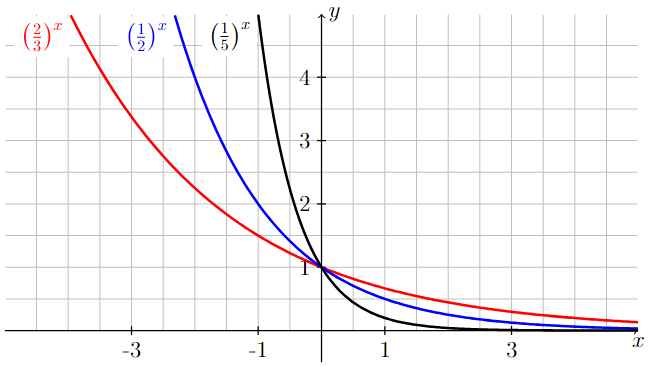
Graphs of exponential decay functions
The graphs of the exponential functions \((2/3)^x\), \((1/2)^x\), and \((1/5)^x\) are all shown below. Since the base associated with each function is between zero and one, each exponential function is decreasing and goes to zero as \(x\) goes to infinity. For this reason, exponential functions with a base between zero and one are referred to as exponential decay functions
Long Text Description
The graphs of 2/3 to the power of x, 1/2 to the power of x, and 1/5 to the power of x are all shown on the same coordinate axes. The values -3, -1, 1, and 3 are marked on the x-axis and the values 1, 2, 3, and 4 are marked on the y-axis.
From left-to-right, the graph of y = 2/3 to the power of x starts very far above the x-axis. The graph quickly decreases to the point (0,1) and continues to decrease for positive values of x, getting closer and closer to the x-axis, but always staying above it. The steepness of the curve decreases from left-to-right.
From left-to-right, the graph of y = 1/2 to the power of x starts very far above the graph of y = 2/3 to the power of x. The graph quickly decreases to the point (0,1), at which point it crosses the graph of y = 2/3 to the power of x. It continues to decrease for positive values of x, staying below the graph of y = 2/3 to the power of x while getting closer and closer to the x-axis from above. The steepness of the curve also decreases from left-to-right.
From left-to-right, the graph of y = 1/5 to the power of x starts very far above the graph of y = 1/2 to the power of x. The graph quickly decreases to the point (0,1), at which point it crosses the graphs of y = 1/2 to the power of x and y = 2/3 to the power of x. It continues to decrease for positive values of x, staying below the graph of y = 1/2 to the power of x while getting closer and closer to the x-axis from above. The steepness of the curve also decreases from left-to-right.
Example 3#
Limits of exponential functions
Evaluate the following limits by first evaluating the limit of the exponent and then applying the corresponding limit property of exponential functions to evaluate the given limit.
\(\lim\limits_{x \to -\infty} 2^{-x^7}\)
Step 1: Evaluate the limit of the exponent.
The exponent, \(-x^7\), goes to positive infinity as \(x\) goes to negative infinity.
Step 2: Evaluate the given limit.
Since the exponent goes to positive infinity and the base is bigger than one, we’ll apply the property that
for \(b>1\). Therefore, \(\lim\limits_{x \to -\infty} 2^{-x^7} = \infty\).
\(\lim\limits_{x \to \infty} 4^{-x^2}\)
Step 1: Evaluate the limit of the exponent.
The exponent, \(-x^2\), goes to negative infinity as \(x\) goes to positive infinity.
Step 2: Evaluate the given limit.
Since the exponent goes to negative infinity and the base is bigger than one, we’ll apply the property that
for \(b>1\). Therefore, \(\lim\limits_{x \to \infty} 4^{-x^2} = 0\).
\(\lim\limits_{x \to 0^+} (1/3)^{5/x}\)
Step 1: Evaluate the limit of the exponent.
The exponent, \(5/x\), goes to positive infinity as \(x\) goes to zero from the right.
Step 2: Evaluate the given limit.
Since the exponent goes to positive infinity and the base is between zero and one, we’ll apply the property that
for \(0<b<1\). Therefore, \(\lim\limits_{x \to 0^+} (1/3)^{5/x} = 0\).
\(\lim\limits_{x \to 0^-} (2/7)^{3/x}\)
Step 1: Evaluate the limit of the exponent.
The exponent, \(3/x\), goes to negative infinity as \(x\) goes to zero from the left.
Step 2: Evaluate the given limit.
Since the exponent goes to negative infinity and the base is between zero and one, we’ll apply the property that
for \(0<b<1\). Therefore, \(\lim\limits_{x \to 0^-} (2/7)^{3/x} = \infty\).
\(\lim\limits_{x \to -\infty} 5^{4/x}\)
Step 1: Evaluate the limit of the exponent.
The exponent, \(4/x\), goes to zero as \(x\) goes to negative infinity.
Step 2: Evaluate the given limit.
Since the exponent goes to zero, we don’t need to apply any of the above properties of exponential functions regarding limits at infinity. Instead, we can make use of the fact that exponential functions are continuous everywhere. In particular, exponential functions are continuous at zero, which means that
for all \(b>0\). Therefore, \(\lim\limits_{x \to -\infty} 5^{4/x} = 1\).
Definition and Properties of Logarithmic Functions#
Definition of a Logarithmic Function
For any constant \(b>0\) and \(b\neq 1\), the logarithmic function with base \(b\), denoted \(\log_b(x)\), is defined by
For example, \(\log_2(8) = 3\) since \(2^3 = 8\).
Properties of Logarithmic Functions
For a function \(y = \log_{b}(x)\), the following properties hold:
Its domain is \((0,\infty)\) and range is \((-\infty,\infty)\).
Its graph passes through the point \((1,0)\) (i.e., \(\log_b(1) = 0\)).
It is continuous on \((0,\infty)\).
If \(b>1\)
\(\log_b(x)\) is increasing on \((0,\infty)\)
\(\lim\limits_{x\to 0^+} \log_b(x) = -\infty\) and \(\lim\limits_{x\to \infty} \log_b(x) = \infty\)
If \(0< b < 1\)
\(\log_b(x)\) is decreasing on \((0,\infty)\)
\(\lim\limits_{x\to 0^+} \log_b(x) = \infty\) and \(\lim\limits_{x\to \infty} \log_b(x) = -\infty\)
A New Domain Restriction
Since the domain of all logarithmic functions is restricted to positive values, whenever we encounter a logarithm, we have to make sure to not take the logarithm of a negative number or of zero. This is the third restriction on a domain we have encountered this semester. The first two restrictions being that we cannot divide by zero and we cannot take the square root of a negative number.
Example 4#
Graphs of logarithmic functions
On the left image below, the graphs of the logarithmic functions \(\log_{5}(x)\), \(\log_{2}(x)\), and \(\log_{3/2}(x)\) are all displayed. Since the base associated with each function is greater than one, each of these logarithmic functions is increasing and goes to positive infinity as \(x\) goes to infinity.
On the right image below, the graphs of the logarithmic functions \(\log_{1/5}(x)\), \(\log_{1/2}(x)\), and \(\log_{2/3}(x)\) are all shown below. Since the base associated with each function is between zero and one, each of these logarithmic functions is decreasing and goes to negative infinity as \(x\) goes to infinity.
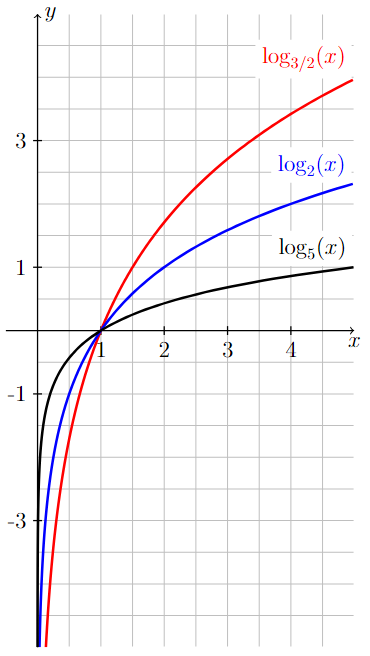
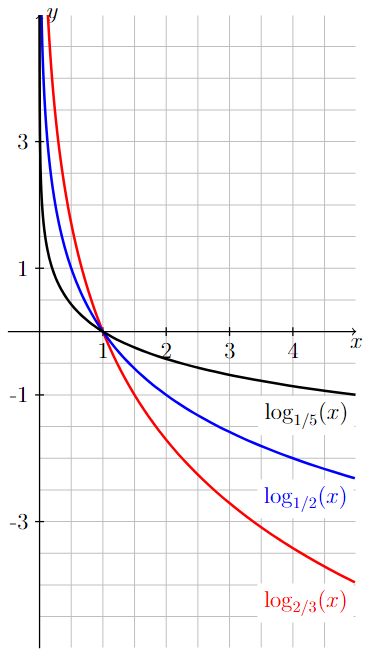
Long Text Description
Two images containing graphs of logarithmic functions are displayed.
On the first image, the graphs of log base 3/2 of x, log base 2 of x, and log base 5 of x are all shown on the same coordinate axes. The values 1, 2, 3, and 4 are marked on the x-axis and the values -3, -1, 1, and 3 are marked on the y-axis.
From left-to-right, the graph of y = log base 3/2 of x starts very far below the x-axis and just to the right of the y-axis. The graph quickly increases to the point (1,0) and continues to increase for values of x greater than one. The steepness of the curve decreases from left-to-right.
From left-to-right, the graph of y = log base 2 of x starts very far below the x-axis and between the y-axis and the graph of y = log base 3/2 of x . The graph quickly increases to the point (1,0), where it crosses the graph of y = log base 3/2 of x. It continues to increase for values of x greater than one, staying below the graph of y = log base 3/2 of x. The steepness of the curve decreases from left-to-right.
From left-to-right, the graph of y = log base 5 of x starts very far below the x-axis and between the y-axis and the graph of y = log base 2 of x . The graph quickly increases to the point (1,0), where it crosses the graph of y = log base 2 of x. It continues to increase for values of x greater than one, staying below the graph of y = log base 2 of x. The steepness of the curve decreases from left-to-right.
On the second image, the graphs of log base 2/3 of x, log base 1/2 of x, and log base 1/5 of x are all shown on the same coordinate axes. The values 1, 2, 3, and 4 are marked on the x-axis and the values -3, -1, 1, and 3 are marked on the y-axis.
From left-to-right, the graph of y = log base 2/3 of x starts very far above the x-axis and just to the right of the y-axis. The graph quickly decreases to the point (1,0) and continues to decrease for values of x greater than 1. The steepness of the curve decreases from left-to-right.
From left-to-right, the graph of y = log base 1/2 of x starts very far above the x-axis and between the y-axis and the graph of y = log base 2/3 of x. The graph quickly decreases to the point (1,0), where it crosses the graph of y = log base 2/3 of x. It continues to decrease for values of x greater than 1, staying above the graph of y = log base 2/3 of x. The steepness of the curve decreases from left-to-right.
From left-to-right, the graph of y = log base 1/5 of x starts very far above the x-axis and between the y-axis and the graph of y = log base 1/2 of x . The graph quickly decreases to the point (1,0), where it crosses the graph of y = log base 1/2 of x. It continues to decrease for values of x greater than one, staying above the graph of y = log base 1/2 of x. The steepness of the curve decreases from left-to-right.
Example 5#
Domain of a logarithmic function
Determine the domain of \(\log_5(3x - 7)\).
Answer
In general, the domain of \(\log_b(f(x))\) consists of all values of \(x\) such that \(f(x) > 0\).
In this case, the domain of \(\log_5(3x - 7)\) consists of all values of \(x\) such that \(3x-7 > 0\). Solving for \(x\) yields \(x > 7/3\). Therefore, the domain of \(\log_5(3x - 7)\) is \((7/3,\infty)\).
For a review of solving inequalities like \(f(x) > 0\), see Solving Inequalities.
Example 6#
Limits of logarithmic functions
Evaluate the following limits by first evaluating the limit of the inner function and then applying the corresponding limit property of logarithmic functions to evaluate the given limit.
\(\lim\limits_{x\to 8^+} \log_{3}(x^2-64) \)
Step 1: Evaluate the limit of the inner function.
The inner function, \(x^2 - 64\), goes to zero from the right as \(x\) goes to eight from the right.
Step 2: Evaluate the given limit.
Since \(x^2 - 64\) goes to zero from the right and the base is bigger than one, we’ll apply the property that
for \(b>1\). Therefore, \(\lim\limits_{x\to 8^+} \log_{3}(x^2-64) = -\infty\).
\(\lim\limits_{x\to 5^-} \log_{1/2}\left(\dfrac{1}{5-x}\right) \)
Step 1: Evaluate the limit of the inner function.
The inner function, \(\dfrac{1}{5-x}\), goes to infinity as \(x\) goes to five from the left.
Step 2: Evaluate the given limit.
Since \(\dfrac{1}{5-x}\) goes to infinity and the base is between zero and one, we’ll apply the property that
for \(0<b<1\). Therefore, \(\lim\limits_{x\to 5^-} \log_{1/2}\left(\dfrac{1}{5-x}\right) = -\infty\).
\(\lim\limits_{x\to \infty} \log_{1/5}\left(\dfrac{2}{x}\right) \)
Step 1: Evaluate the limit of the inner function.
The inner function, \(\dfrac{2}{x}\), goes to zero from the right as \(x\) goes to infinity.
Step 2: Evaluate the given limit.
Since \(\dfrac{2}{x}\) goes to zero from the right and the base is between zero and one, we’ll apply the property that
for \(0<b<1\). Therefore, \(\lim\limits_{x\to \infty} \log_{1/5}\left(\dfrac{2}{x}\right) = \infty\).
The Natural Exponential and Logarithmic Functions#
Definition
The natural exponential function, denoted \(e^x\), is an exponential function with base \(e \approx 2.71828\). The exact value of \(e\) can be defined in a variety of different ways, one of which is the following:
The natural logarithmic function, denoted \(\ln(x)\), is the logarithmic function with base \(e\) (i.e., \(\ln(x) = \log_e(x)\)).
Limit Properties of the Natural Exponential and Logarithmic Functions
The functions \(e^x\) and \(\ln(x)\) satisfy the corresponding properties listed above for all exponential and logarithmic functions. And in particular, since \(e>1\), we have the following.
\(e^x\) is increasing on \((-\infty,\infty)\)
\(\lim\limits_{x\to -\infty} e^x = 0\) and \(\lim\limits_{x\to \infty} e^x = \infty\)
\(\ln(x)\) is increasing on \((0,\infty)\)
\(\lim\limits_{x\to 0^+} \ln(x) = -\infty\) and \(\lim\limits_{x\to \infty} \ln(x) = \infty\)
Example 7#
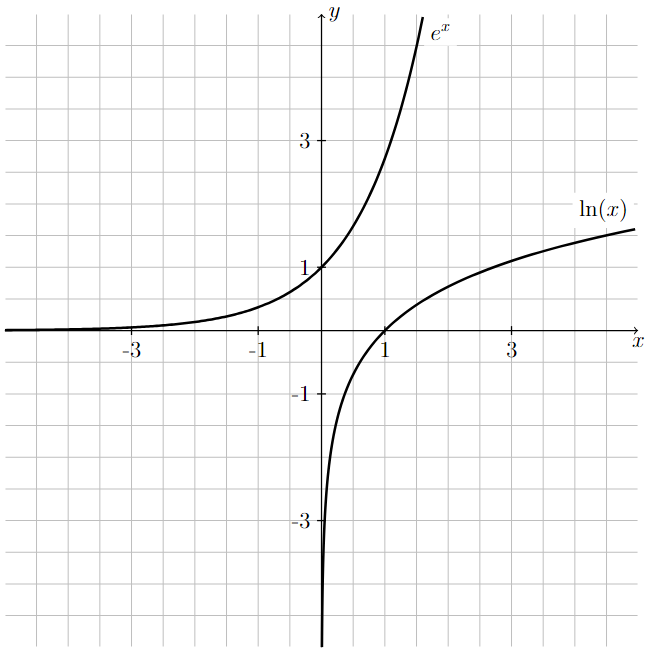
Graphs of the natural exponential and logarithmic functions
The graphs of \(y=e^x\) and \(y = \ln(x)\) are shown below.
Long Text Description
The graph of y = e^x and y = ln(x) are both shown on the same coordinate axes. The values -3, -1, 1, and 3 are marked on both the x-axis and the y-axis.
From left-to-right, the graph of y = e^x starts very close to and above the x-axis. The graph increases to the point (0,1) and continues to increase for positive values of x. The steepness of the curve also increases from left-to-right.
From bottom-to-top, the graph of y = ln(x) starts very close to and to the right of the y-axis. The graph increases to the point (1,0) and continues to increase for values of x greater than 1. The steepness of the curve decreases from bottom-to-top.
Example 8#
Limits of \(e^x\) and \(\ln(x)\)
Evaluate the following limits.
\(\lim\limits_{x \to \infty} e^{-x^7}\)
Step 1: Evaluate the limit of the exponent.
The exponent, \(-x^7\), goes to negative infinity as \(x\) goes to positive infinity.
Step 2: Evaluate the given limit.
Since the exponent goes to negative infinity, we’ll apply the property that
Therefore, \(\lim\limits_{x \to \infty} e^{-x^7} = 0\).
\(\lim\limits_{x \to -\infty} e^{-x^2}\)
Step 1: Evaluate the limit of the exponent.
The exponent, \(-x^2\), goes to negative infinity as \(x\) goes to negative infinity.
Step 2: Evaluate the given limit.
Since the exponent goes to negative infinity, we’ll apply the property that
Therefore, \(\lim\limits_{x \to \infty} e^{-x^2} = 0\).
\(\lim\limits_{x \to 0^+} e^{5/x}\)
Step 1: Evaluate the limit of the exponent.
The exponent, \(5/x\), goes to positive infinity as \(x\) goes to zero from the right.
Step 2: Evaluate the given limit.
Since the exponent goes to positive infinity, we’ll apply the property that
Therefore, \(\lim\limits_{x \to 0^+} e^{5/x} = \infty\).
\(\lim\limits_{x \to 0^-} e^{3/x}\)
Step 1: Evaluate the limit of the exponent.
The exponent, \(3/x\), goes to negative infinity as \(x\) goes to zero from the left.
Step 2: Evaluate the given limit.
Since the exponent goes to negative infinity, we’ll apply the property that
Therefore, \(\lim\limits_{x \to 0^-} e^{3/x} = 0\).
\(\lim\limits_{x \to -\infty} e^{4/x}\)
Step 1: Evaluate the limit of the exponent.
The exponent, \(4/x\), goes to zero as \(x\) goes to negative infinity.
Step 2: Evaluate the given limit.
Since the exponent goes to zero, we don’t need to apply any of the above properties of exponential functions regarding limits at infinity. Instead, we can make use of the fact that \(e^x\) is continuous everywhere. In particular, \(e^x\) is continuous at zero, which means that
Therefore, \(\lim\limits_{x \to -\infty} e^{4/x} = 1\).
\(\lim\limits_{x\to 1^-} \ln(1-x^2)\)
Step 1: Evaluate the limit of the inner function.
The inner function, \(1-x^2\), goes to zero from the right as \(x\) goes to one from the left.
Step 2: Evaluate the given limit.
Since \(1-x^2\) goes to zero from the right, we’ll apply the property that
Therefore, \(\lim\limits_{x\to 1^-} \ln(1 - x^2) = -\infty\).
\(\lim\limits_{x\to 3^+} \ln\left(\dfrac{1}{x - 3}\right) \)
Step 1: Evaluate the limit of the inner function.
The inner function, \(\dfrac{1}{x-3}\), goes to infinity as \(x\) goes to three from the right.
Step 2: Evaluate the given limit.
Since \(\dfrac{1}{x-3}\) goes to infinity, we’ll apply the property that
Therefore, \(\lim\limits_{x\to 3^+} \ln\left(\dfrac{1}{x-3}\right) = \infty\).
\(\lim\limits_{x\to \infty} \ln\left(\dfrac{2}{x}\right)\)
Step 1: Evaluate the limit of the inner function.
The inner function, \(\dfrac{2}{x}\), goes to zero from the right as \(x\) goes to infinity.
Step 2: Evaluate the given limit.
Since \(\dfrac{2}{x}\) goes to zero from the right, we’ll apply the property that
Therefore, \(\lim\limits_{x\to \infty} \ln\left(\dfrac{2}{x}\right) = -\infty\).
\(\lim\limits_{x\to -\infty} \ln\left(\dfrac{5x^2 + 3}{7x^2 - 1}\right)\)
Step 1: Evaluate the limit of the inner function.
The inner function, \(\dfrac{5x^2 + 3}{7x^2 - 1}\), goes to \(5/7\) as \(x\) goes to negative infinity.
Step 2: Evaluate the given limit.
Since \(\dfrac{5x^2 + 3}{7x^2 - 1}\) goes to \(5/7\), we don’t need to apply any of the above properties of logarithmic functions regarding infinite limits. Instead, we can make use of the fact that \(\ln(x)\) is continuous on \((0,\infty)\). In particular, \(\ln(x)\) is continuous at \(5/7\), which means that
Therefore, \(\lim\limits_{x\to -\infty} \ln\left(\dfrac{5x^2 + 3}{7x^2 - 1}\right) = \ln(5/7)\).