Logarithmic Functions#
Definition and Properties of Logarithmic Functions#
Definition of a Logarithmic Function
For any constant \(b>0\) and \(b\neq 1\), the logarithmic function with base \(b\), denoted \(\log_b(x)\), is defined by
For example, \(\log_2(8) = 3\) since \(2^3 = 8\).
Properties of Logarithmic Functions
For a function \(y = \log_{b}(x)\), the following properties hold:
Its domain is \((0,\infty)\) and range is \((-\infty,\infty)\).
Its graph passes through the point \((1,0)\) (i.e., \(\log_b(1) = 0\)).
It is continuous on \((0,\infty)\).
If \(b>1\)
\(\log_b(x)\) is increasing on \((0,\infty)\)
\(\lim\limits_{x\to 0^+} \log_b(x) = -\infty\) and \(\lim\limits_{x\to \infty} \log_b(x) = \infty\)
If \(0< b < 1\)
\(\log_b(x)\) is decreasing on \((0,\infty)\)
\(\lim\limits_{x\to 0^+} \log_b(x) = \infty\) and \(\lim\limits_{x\to \infty} \log_b(x) = -\infty\)
A New Domain Restriction
Since the domain of all logarithmic functions is restricted to positive values, whenever we encounter a logarithm, we have to make sure to not take the logarithm of a negative number or of zero. This is the third restriction on a domain we have encountered this semester. The first two restrictions being that we cannot divide by zero and we cannot take the square root of a negative number.
Video Resource

How to Evaluate Logarithms (Links to an external site)
A review of the definition of a logarithm and how to use that definition to evaluate logarithms.
Example 1#
Graphs of logarithmic functions
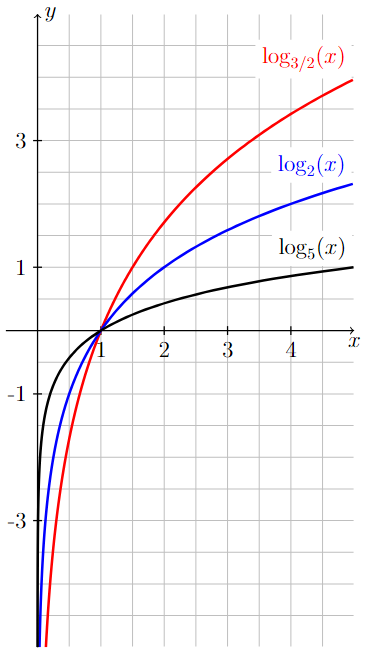
On the left image below, the graphs of the logarithmic functions \(\log_{5}(x)\), \(\log_{2}(x)\), and \(\log_{3/2}(x)\) are all displayed. Since the base associated with each function is greater than one, each of these logarithmic functions is increasing and goes to positive infinity as \(x\) goes to infinity.
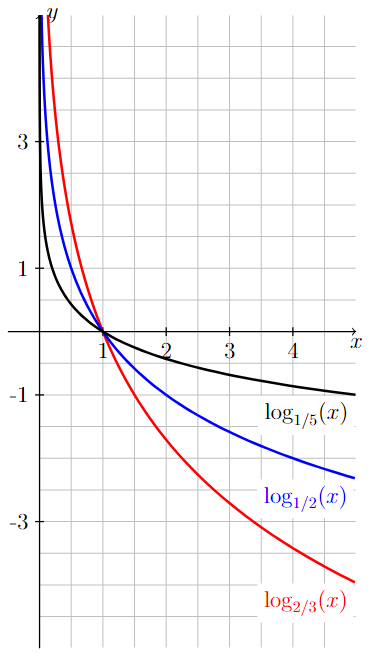
On the right image below, the graphs of the logarithmic functions \(\log_{1/5}(x)\), \(\log_{1/2}(x)\), and \(\log_{2/3}(x)\) are all shown below. Since the base associated with each function is between zero and one, each of these logarithmic functions is decreasing and goes to negative infinity as \(x\) goes to infinity.
Long Text Description
Two images containing graphs of logarithmic functions are displayed.
On the first image, the graphs of log base 3/2 of x, log base 2 of x, and log base 5 of x are all shown on the same coordinate axes. The values 1, 2, 3, and 4 are marked on the x-axis and the values -3, -1, 1, and 3 are marked on the y-axis.
From left-to-right, the graph of y = log base 3/2 of x starts very far below the x-axis and just to the right of the y-axis. The graph quickly increases to the point (1,0) and continues to increase for values of x greater than one. The steepness of the curve decreases from left-to-right.
From left-to-right, the graph of y = log base 2 of x starts very far below the x-axis and between the y-axis and the graph of y = log base 3/2 of x . The graph quickly increases to the point (1,0), where it crosses the graph of y = log base 3/2 of x. It continues to increase for values of x greater than one, staying below the graph of y = log base 3/2 of x. The steepness of the curve decreases from left-to-right.
From left-to-right, the graph of y = log base 5 of x starts very far below the x-axis and between the y-axis and the graph of y = log base 2 of x . The graph quickly increases to the point (1,0), where it crosses the graph of y = log base 2 of x. It continues to increase for values of x greater than one, staying below the graph of y = log base 2 of x. The steepness of the curve decreases from left-to-right.
On the second image, the graphs of log base 2/3 of x, log base 1/2 of x, and log base 1/5 of x are all shown on the same coordinate axes. The values 1, 2, 3, and 4 are marked on the x-axis and the values -3, -1, 1, and 3 are marked on the y-axis.
From left-to-right, the graph of y = log base 2/3 of x starts very far above the x-axis and just to the right of the y-axis. The graph quickly decreases to the point (1,0) and continues to decrease for values of x greater than 1. The steepness of the curve decreases from left-to-right.
From left-to-right, the graph of y = log base 1/2 of x starts very far above the x-axis and between the y-axis and the graph of y = log base 2/3 of x. The graph quickly decreases to the point (1,0), where it crosses the graph of y = log base 2/3 of x. It continues to decrease for values of x greater than 1, staying above the graph of y = log base 2/3 of x. The steepness of the curve decreases from left-to-right.
From left-to-right, the graph of y = log base 1/5 of x starts very far above the x-axis and between the y-axis and the graph of y = log base 1/2 of x . The graph quickly decreases to the point (1,0), where it crosses the graph of y = log base 1/2 of x. It continues to decrease for values of x greater than one, staying above the graph of y = log base 1/2 of x. The steepness of the curve decreases from left-to-right.
Example 2#
Domain of a logarithmic function
Determine the domain of \(\log_5(3x - 7)\).
Answer
In general, the domain of \(\log_b(f(x))\) consists of all values of \(x\) such that \(f(x) > 0\).
In this case, the domain of \(\log_5(3x - 7)\) consists of all values of \(x\) such that \(3x-7 > 0\). Solving for \(x\) yields \(x > 7/3\). Therefore, the domain of \(\log_5(3x - 7)\) is \((7/3,\infty)\).
For a review of solving inequalities like \(f(x) > 0\), see Solving Inequalities.
Example 3#
Limits of logarithmic functions
Evaluate the following limits by first evaluating the limit of the inner function and then applying the corresponding limit property of logarithmic functions to evaluate the given limit.
\(\lim\limits_{x\to 8^+} \log_{3}(x^2-64) \)
Step 1: Evaluate the limit of the inner function.
The inner function, \(x^2 - 64\), goes to zero from the right as \(x\) goes to eight from the right.
Step 2: Evaluate the given limit.
Since \(x^2 - 64\) goes to zero from the right and the base is bigger than one, we’ll apply the property that
for \(b>1\). Therefore, \(\lim\limits_{x\to 8^+} \log_{3}(x^2-64) = -\infty\).
\(\lim\limits_{x\to 5^-} \log_{1/2}\left(\dfrac{1}{5-x}\right) \)
Step 1: Evaluate the limit of the inner function.
The inner function, \(\dfrac{1}{5-x}\), goes to infinity as \(x\) goes to five from the left.
Step 2: Evaluate the given limit.
Since \(\dfrac{1}{5-x}\) goes to infinity and the base is between zero and one, we’ll apply the property that
for \(0<b<1\). Therefore, \(\lim\limits_{x\to 5^-} \log_{1/2}\left(\dfrac{1}{5-x}\right) = -\infty\).
\(\lim\limits_{x\to \infty} \log_{1/5}\left(\dfrac{2}{x}\right) \)
Step 1: Evaluate the limit of the inner function.
The inner function, \(\dfrac{2}{x}\), goes to zero from the right as \(x\) goes to infinity.
Step 2: Evaluate the given limit.
Since \(\dfrac{2}{x}\) goes to zero from the right and the base is between zero and one, we’ll apply the property that
for \(0<b<1\). Therefore, \(\lim\limits_{x\to \infty} \log_{1/5}\left(\dfrac{2}{x}\right) = \infty\).
